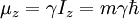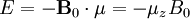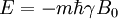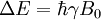To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Nuclear magnetic resonance
Nuclear magnetic resonance (NMR) is a physical phenomenon based upon the quantum mechanical magnetic properties of an atom's nucleus. NMR also commonly refers to a family of scientific methods that exploit nuclear magnetic resonance to study molecules. All nuclei that contain odd numbers of protons or neutrons have an intrinsic magnetic moment and angular momentum. The most commonly measured nuclei are hydrogen-1 (the most receptive isotope at natural abundance) and carbon-13, although nuclei from isotopes of many other elements (e.g. 15N, 14N 19F, 31P, 17O, 29Si, 10B, 11B, 23Na, 35Cl, 195Pt) can also be observed. NMR resonant frequencies for a particular substance are directly proportional to the strength of the applied magnetic field, in accordance with the equation for the Larmor precession frequency. NMR studies magnetic nuclei by aligning them with an applied constant magnetic field and perturbing this alignment using an alternating electric field, those fields being orthogonal. The resulting response to the perturbing magnetic field is the phenomenon that is exploited in NMR spectroscopy and magnetic resonance imaging, which use very powerful applied magnetic fields in order to achieve high resolution spectra, details of which are described by the chemical shift and the Zeeman effect. NMR phenomena are also utilised in low field NMR and earth's field NMR spectrometers, and some kinds of magnetometer. Product highlight
HistoryDiscoveryNuclear magnetic resonance was first described and measured in molecular beams by Isidor Rabi in 1938.[1] Eight years later, in 1946, Felix Bloch and Edward Mills Purcell refined the technique for use on liquids and solids, for which they shared the Nobel Prize in physics in 1952. Purcell had worked on the development and application of RADAR during World War II at Massachusetts Institute of Technology's Radiation Laboratory. His work during that project on the production and detection of radiofrequency energy, and on the absorption of such energy by matter, preceded his discovery of NMR. They noticed that magnetic nuclei, like 1H and 31P, could absorb RF energy when placed in a magnetic field of a strength specific to the identity of the nuclei. When this absorption occurs, the nucleus is described as being in resonance. Interestingly, for analytical scientists, different atoms within a molecule resonate at different frequencies at a given field strength. The observation of the resonance frequencies of a molecule allows a user to discover structural information about the molecule. The development of nuclear magnetic resonance as a technique of analytical chemistry and biochemistry parallels the development of electromagnetic technology and its introduction into civilian use. Theory of nuclear magnetic resonanceNuclear spin and magnetsThe elementary particles, neutrons and protons, composing an atomic nucleus, have the intrinsic quantum mechanical property of spin. The overall spin of the nucleus is determined by the spin quantum number I. If the number of both the protons and neutrons in a given isotope are even then I = 0, i.e. there is no overall spin; just as electrons pair up in atomic orbitals, so do even numbers of protons and neutrons (which are also spin ½ particles and hence fermions) pair up giving zero overall spin. In other cases, however, the overall spin is non-zero. For example 27Al has an overall spin I = 5/2. A non-zero spin is associated with a non-zero magnetic moment, μ, via where the proportionality constant, γ, is the gyromagnetic ratio. It is this magnetic moment that is exploited in NMR. Electron spin resonance is a related technique which exploits the spin of electrons instead of nuclei. The basic principles are otherwise similar. Values of spin angular momentumThe angular momentum associated with nuclear spin is quantized. This means both that the magnitude of angular momentum is quantized (i.e. I can only take on a restricted range of values), and also that the 'orientation' of the associated angular momentum is quantized. The associated quantum number is known as the magnetic quantum number, m, and can take values from +I to –I in integral steps. Hence for any given nucleus, there is a total of 2I+1 angular momentum states. The z component of the angular momentum vector, Iz, is therefore: where The z component of the magnetic moment is simply Spin behavior in a magnetic fieldConsider nuclei which have a spin of one-half, like 1H, 13C or 19F. The nucleus has two possible spin states: m = ½ or m = -½ (also referred to as up and down or α and β, respectively). The energies of these states are degenerate—that is to say that they are the same. Hence the populations of the two states (i.e. number of atoms in the two states) will be exactly equal at thermal equilibrium. If a nucleus is placed in a magnetic field, however, the interaction between the nuclear magnetic moment and the external magnetic field mean the two states no longer have the same energy. The energy of a magnetic moment μ when in a magnetic field B0 (the zero subscript is used to distinguish this magnetic field from any other applied field) is given by the negative scalar product of the vectors: where the magnetic field has been oriented along the z axis. Hence As a result the different nuclear spin states have different energies in a non-zero magnetic field. In hand-waving terms, we can talk about the two spin states of a spin ½ as being aligned either with or against the magnetic field. If γ is positive (true for most isotopes) then m = ½ is the lower energy state. The energy difference between the two states is and this difference results in a small population bias toward the lower energy state. ResonanceResonant absorption will occur when electromagnetic radiation of the correct frequency to match this energy difference is applied. The energy of a photon is E = hν, where ν is its frequency. Hence absorption will occur when These frequencies typically correspond to the radio frequency range of the electromagnetic spectrum. It is this resonant absorption that is detected in NMR. Nuclear shieldingIt might appear from the above that all nuclei of the same nuclide (and hence the same γ) would resonate at the same frequency. This is not the case. The most important perturbation of the NMR frequency for applications of NMR is the 'shielding' effect of the surrounding electrons. In general, this electronic shielding reduces the magnetic field at the nucleus (which is what determines the NMR frequency). As a result the energy gap is reduced, and the frequency required to achieve resonance is also reduced. This shift of the NMR frequency due to the chemical environment is called the chemical shift, and it explains why NMR is a direct probe of chemical structure. Unless the local symmetry is particularly high, the shielding effect depends on the orientation of the molecule with respect to the external field. In solid-state NMR, magic angle spinning is required to average out this orientation dependence. This is unnecessary in conventional NMR of molecules in solution since rapid molecular tumbling averages out the anisotropic component of the chemical shift. Relaxation
The process called population relaxation refers to nuclei that return to the thermodynamic state in the magnet. This process is also called T1 relaxation, where T1 refers to the mean time for an individual nucleus to return to its equilibrium state. Once the population is relaxed, it can be probed again, since it is in the initial state. The precessing nuclei can also fall out of alignment with each other (returning the net magnetization vector to a nonprecessing field) and stop producing a signal. This is called T2 relaxation. It is possible to be in this state and not have the population difference required to give a net magnetization vector at its thermodynamic state. Because of this, T1 is always larger (slower) than T2. This happens because some of the spins were flipped by the pulse and will remain so until they have undergone population relaxation. In practice, the T2 time is the life time of the observed NMR signal, the free induction decay. In the NMR spectrum, meaning the Fourier transform of the free induction decay, the T2 time defines the width of the NMR signal. Thus, a nucleus having a large T2 time gives rise to a sharp signal, whereas nuclei with shorter T2 times give rise to more broad signals. The length of T1 and T2 is closely related to molecular motion. NMR spectroscopyNMR spectroscopy is one of the principal techniques used to obtain physical, chemical, electronic and structural information about molecules due to the chemical shift and Zeeman effect on the resonant frequencies of the nuclei. It is a powerful technique that can provide detailed information on the topology, dynamics and three-dimensional structure of molecules in solution and the solid state. Also, nuclear magnetic resonance is one of the techniques that has been used to build elementary quantum computers. Continuous wave (CW) spectroscopyIn its first few decades, nuclear magnetic resonance spectrometers used a technique known as continuous-wave (CW) spectroscopy. Although NMR spectra could be obtained using a fixed magnetic field and sweeping the frequency of the electromagnetic radiation, this more typically involved using a fixed frequency source and varying the current (and hence magnetic field) in an electromagnet to observe the resonant absorption signals. (This is the origin of the now anachronistic but still common "high" and "low" field terminology for low frequency and high frequency regions respectively of the NMR spectrum.) CW spectroscopy is inefficient in comparison to Fourier techniques (see below) as it probes the NMR response at individual frequencies in succession. As the NMR signal is intrinsically weak, the observed spectra suffer from a poor signal-to-noise ratio (S/N). This can be mitigated by signal averaging i.e. adding the spectra from repeated measurements. While the NMR signal is constant between scans and so adds linearly, the random noise adds more slowly — as the square-root of the number of spectra (see Random walk). Hence the overall ratio of the signal to the noise increases as the square-root of the number of spectra measured. Fourier spectroscopyMost applications of NMR involve full NMR spectra, that is, the intensity of the NMR signal as a function of frequency. Early attempts to acquire the NMR spectrum more efficiently than simple CW methods involved irradiating simultaneously with more than one frequency. It was soon realised, however, that a simpler solution was to use short pulses of radio-frequency (centred at the middle of the NMR spectrum). In simple terms, a short square pulse of a given "carrier" frequency "contains" a range of frequencies centred about the carrier frequency, with the range of excitation (bandwidth) being inversely proportional to the pulse duration (the Fourier transform of an approximate square wave contains contributions from all the frequencies in the neighborhood of the principal frequency). The restricted range of the NMR frequencies made it relatively easy to use RF pulses to excite the entire NMR spectrum. Applying such a pulse to a set of nuclear spins simultaneously excites all the NMR transitions. In terms of the net magnetisation vector, this corresponds to tilting the magnetisation vector away from its equilibrium position (aligned along the external magnetic field). The out-of-equilibrium magnetisation vector precesses about the external magnetic field at the NMR frequency of the spins. This oscillating magnetisation induces a current in a nearby pickup coil, creating an electrical signal oscillating at the NMR frequency. This signal is known as the free induction decay (FID) and contains the sum of the NMR responses from all the excited spins. In order to obtain the frequency-domain NMR spectrum (intensity vs. frequency) this time-domain signal (intensity vs. time) must be Fourier transformed. Fortunately the development of FT-NMR coincided with the development of digital computers and Fast Fourier Transform algorithms. Richard R. Ernst was one of the pioneers of pulse (FT) NMR and won a Nobel Prize in chemistry in 1991 for his work on FT-NMR and his development of multi-dimensional NMR (see below). Multi-dimensionalThe use of pulses of different shapes, frequencies and durations in specifically-designed patterns or pulse sequences allows the spectroscopist to extract many different types of information about the molecule. Multi-dimensional nuclear magnetic resonance spectroscopy is a kind of FT-NMR in which there are at least two pulses and, as the experiment is repeated, the pulse sequence is varied. In multidimensional nuclear magnetic resonance there will be a sequence of pulses and, at least, one variable time period. In three dimensions, two time sequences will be varied. In four dimensions, three will be varied. There are many such experiments. In one, these time intervals allow—among other things—magnetization transfer between nuclei and, therefore, the detection of the kinds of nuclear-nuclear interactions that allowed for the magnetization transfer. Interactions that can be detected are usually classified into two kinds. There are through-bond interactions and through-space interactions, the latter usually being a consequence of the nuclear Overhauser effect. Experiments of the nuclear-Overhauser variety may establish distances between atoms. Although the fundamental concept of 2D NMR was proposed by the Belgian scientist Jean Jeener, professor at the Free University of Brussels (now split into the Université Libre de Bruxelles and the Vrije Universiteit Brussel), this idea was largely developed by Richard Ernst who won the 1991 Nobel prize in Chemistry for his work in FT and multi-dimensional NMR. Multi-dimensional NMR experiments were further developed into powerful methodologies for studying biomolecules in solution, in particular for the determination of the structure of biopolymers such as proteins or even small nucleic acids. Kurt Wüthrich shared the 2002 Nobel Prize in Chemistry for his work in protein nuclear magnetic resonance spectroscopy. SolidsThis technique complements biopolymer X-ray crystallography in that it is frequently applicable to biomolecules in a liquid or liquid crystal phase, whereas crystallography, as the name implies, is performed on molecules in a solid phase. Though nuclear magnetic resonance is used to study solids, extensive atomic-level biomolecular structural detail is especially challenging to obtain in the solid state. There is no signal averaging by thermal motion in the solid state, where molecules are held still, each in a slightly different electronic environment, giving a different signal. This variation in electronic environment lowers resolution greatly and makes interpretation more difficult. Raymond Andrew was a pioneer in the development of high-resolution solid-state nuclear magnetic resonance. He introduced the magic angle spinning (MAS) technique and allowed for an increase in resolution by several orders of magnitude. In MAS, the sample is averaged by spinning it at several kilohertz. Alex Pines together with John S. Waugh revolutionized the area with the introduction of the cross-polarization technique in order to enhance low abundance and sensitivity nuclei. SensitivityBecause the intensity of nuclear magnetic resonance signals and, hence, the sensitivity of the technique depends on the strength of the magnetic field the technique has also advanced over the decades with the development of more powerful magnets. Advances made in audio-visual technology have also improved the signal-generation and processing capabilities of newer machines. The sensitivity of nuclear magnetic resonance signals is also dependent—as noted above—on the presence of a magnetically-susceptible nuclide and, therefore, either on the natural abundance of such nuclides or on the ability of the experimentalist to artificially enrich the molecules, under study, with such nuclides. The most abundant naturally-occurring isotopes of hydrogen and phosphorus—for instance—are both magnetically susceptible and readily useful for nuclear magnetic resonance spectroscopy. In contrast, carbon and nitrogen have useful isotopes but which occur only in very low natural abundance. Other limitations on sensitivity arise from the quantum-mechanical nature of the phenomenon. For quantum states separated by energy equivalent to radio frequencies, thermal energy from the environment causes the populations of the states to be close to equal. Since incoming radiation is equally likely to cause stimulated emission (a transition from the upper to the lower state) as absorption, the NMR effect depends on an excess of nuclei in the lower states. Several factors can reduce sensitivity, including
IsotopesMany chemical elements can be used for NMR analysis. [1]
ApplicationsMedicineThe use of nuclear magnetic resonance best known to the general public is in magnetic resonance imaging for medical diagnosis, however, it is also widely used in chemical studies, notably in NMR spectroscopy such as proton NMR and carbon-13 NMR. Biochemical information can also be obtained from living tissue (e.g human brain tumours) with the technique known as in vivo magnetic resonance spectroscopy. These studies are possible because nuclei are surrounded by orbiting electrons, which are also spinning charged particles such as magnets and, so, will partially shield the nuclei. The amount of shielding depends on the exact local environment. For example, a hydrogen bonded to an oxygen will be shielded differently than a hydrogen bonded to a carbon atom. In addition, two hydrogen nuclei can interact via a process known as spin-spin coupling, if they are on the same molecule, which will split the lines of the spectra in a recognisable way. ChemistryBy studying the peaks of nuclear magnetic resonance spectra, skilled chemists can determine the structure of many compounds. It can be a very selective technique, distinguishing among many atoms within a molecule or collection of molecules of the same type but which differ only in terms of their local chemical environment. By studying T2* information a chemist can determine the identity of a compound by comparing the observed nuclear precession frequencies to known frequencies. Further structural data can be elucidated by observing spin-spin coupling, a process by which the precession frequency of a nucleus can be influenced by the magnetization transfer from nearby nuclei. Spin-spin coupling is most commonly observed in NMR involving common isotopes, such as Hydrogen-1 (HNMR). T2 information can give information about dynamics and molecular motion. Because the nuclear magnetic resonance timescale is rather slow, compared to other spectroscopic methods, changing the temperature of a T2* experiment can also give information about fast reactions, such as the Cope rearrangement or about structural dynamics, such as ring-flipping in cyclohexane. An example of nuclear magnetic resonance being used in the determination of a structure is that of buckminsterfullerene. This now famous form of carbon has 60 carbon atoms forming a sphere. The carbon atoms are all in identical environments and so should see the same internal H field. Unfortunately, buckminsterfullerene contains no hydrogen and so 13C nuclear magnetic resonance has to be used. 13C spectra require longer acquisition times since carbon-13 is not the common isotope of carbon (unlike hydrogen, where 1H is the common isotope). However, in 1990 the spectrum was obtained by R. Taylor and co-workers at the University of Sussex and was found to contain a single peak, confirming the unusual structure of C60.[2] Non-destructive testingNuclear magnetic resonance is extremely useful for analyzing samples non-destructively. Radio waves and static magnetic fields easily penetrate many types of matter and anything that is not inherently ferromagnetic. For example, various expensive biological samples, such as nucleic acids, including RNA and DNA, or proteins, can be studied using nuclear magnetic resonance for weeks or months before using destructive biochemical experiments. This also makes nuclear magnetic resonance a good choice for analyzing dangerous samples. Data acquisition in the petroleum industryAnother use for nuclear magnetic resonance is data acquisition in the petroleum industry for petroleum and natural gas exploration and recovery. A borehole is drilled into rock and sedimentary strata into which nuclear magnetic resonance logging equipment is lowered. Nuclear magnetic resonance analysis of these boreholes is used to measure rock porosity, estimate permeability from pore size distribution and identify pore fluids (water, oil and gas). These instruments are typically low field NMR spectrometers. Process controlNMR has now entered the arena of real-time process control and process optimization in oil refineries and petrochemical plants. Two different types of NMR analysis are utilized to provide real time analysis of feeds and products in order to control and optimize unit operations. Time-domain NMR (TD-NMR) spectrometers operating at low field (2-20 MHz for 1H) yield free induction decay data that can be used to determine absolute hydrogen content values, rheological information, and component composition. These spectrometers are used in mining, polymer production, cosmetics and food manufacturing as well as coal analysis. High resolution FT-NMR spectrometers operating in the 60 MHz range with shielded permanent magnet systems yield high resolution 1H NMR spectra of refinery and petrochemical streams. The variation observed in these spectra with changing physical and chemical properties is modelled utilizing chemometrics to yield predictions on unknown samples. The prediction results are provided to control systems via analogue or digital outputs from the spectrometer. Earth's field NMRIn the Earth's magnetic field, NMR frequencies are in the audio frequency range. EFNMR is typically stimulated by applying a relatively strong dc magnetic field pulse to the sample and, following the pulse, analysing the resulting low frequency alternating magnetic field that occurs in the earth's magnetic field due to free induction decay (FID). These effects are exploited in some types of magnetometers, and in EFNMR spectrometers. Their inexpensive portable nature makes these spectrometers valuable for field use and for teaching. MagnetometersVarious magnetometers use NMR effects to measure magnetic fields, including Proton precession magnetometers (PPM) and Overhauser magnetometers. See also Earth's field NMR. Makers of NMR equipmentMajor NMR instrument makers include Bruker, General Electric, JEOL, Kimble Chase, Philips, Siemens AG, and Varian, Inc. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Nuclear_magnetic_resonance". A list of authors is available in Wikipedia. |





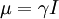
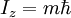
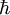 is Planck's reduced constant.
is Planck's reduced constant.