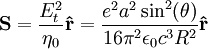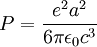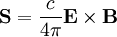To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Larmor formulaIn physics, in the area of electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J. Larmor in 1897, in the context of the wave theory of light. When accelerating or decelerating, any charged particle (such as an electron) radiates away energy in the form of electromagnetic waves. For velocities that are small relative to the speed of light, the total power radiated is given by the Larmor formula: where a is the acceleration, e is the charge, and c is the speed of light. Product highlight
DerivationDerivation 1: Fields of a moving charge
Retarded potential solutionsIn the case that there are no boundaries surrounding the sources, the retarded solutions for the scalar and vector potentials (cgs units) of the nonhomogeneous wave equations are (see Nonhomogeneous electromagnetic wave equation) and where is a Dirac delta function and the current and charge densities are for a particle at Electric and magnetic fieldsThe scalar and vector potentials are related to the electric and magnetic fields by
The fields can be written where
and the terms on the right are evaluated at the retarded time
The second term, proportional to the acceleration, represents a spherically moving light wave. The first term falls of as the square of the distance and represents a wave that decays with distance. Derivation 2: Using Edward M. Purcell approachThe full derivation can be found in http://physics.weber.edu/schroeder/mrr/MRRtalk.html Here is an explanation which can help understanding the above page. This approach is based on the finite speed of light. A charge moving with constant velocity has a radial electric field Er (at distance R from the charge), always emerging from the future position of the charge, and there is no tangential component of the electric field (Et = 0). This future position is completely deterministic as long as the velocity is constant. When the velocity of the charge changes, (say it bounces back during a short time) the future position "jumps", so from this moment and on, the radial electric field Er emerges from a new position. Given the fact that the electric field must be continuous, a non-zero tangential component of the electric field Et appears, which decreases like 1 / R (unlike the radial component which decreases like 1 / R2). Hence, at large distances from the charge, the radial component is negligible relative to the tangential component, and in addition to that, fields which behave like 1 / R2 cannot radiate, because the Poynting vector associated with them will behave like 1 / R4. The tangential component comes out (SI units):
And to obtain the Larmour formula, one has to integrate over all angles, at large distance R from the charge, the Poynting vector associated with Et, which is: giving (SI units) Issues and implicationsEnergy fluxThe energy flux from the electromagnetic wave is given by the Poynting vector (cgs units). Integration of the power over the surface of a sphere centered on the emitting particle yields the Larmor power formula in the nonrelativistic limit. Radiation reactionThe radiation from a charged particle carries energy and momentum. In order to satisfy energy and momentum conservation, the charged particle must experience a recoil at the time of emission. The radiation must exert an additional force on the charged particle. This force is known as the Abraham-Lorentz force in the nonrelativistic limit and the Abraham-Lorentz-Dirac force in the relativistic limit. Atomic physicsA classical electron orbiting a nucleus experiences acceleration and should radiate. Consequently the electron loses energy and the electron should eventually spiral into the nucleus. Atoms, according to classical mechanics, are consequently unstable. This certainly is violation of observation. The problem is resolved with a quantum mechanical description of atomic physics. See also
References
Categories: Atomic physics | Electromagnetic radiation |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Larmor_formula". A list of authors is available in Wikipedia. |


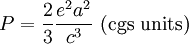



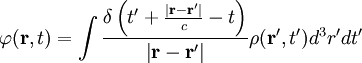
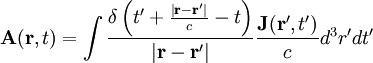
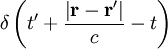
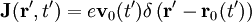
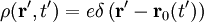
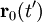 traveling with velocity
traveling with velocity 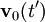 .
.
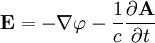
 .
.
![\mathbf{E}(\mathbf{r}, t) = e \left [ { { \left ( \mathbf{n} - { \mathbf{v}_0 \over c } \right ) \left ( 1-\beta^2 \right ) } \over { \kappa^3 R^2 } } \right ]_{\mbox{ret} } + {e \over c} \left [ { { \mathbf{n} \times \left ( \mathbf{n} - { \mathbf{v}_0 \over c } \right ) \times { \mathbf{a} \over c } } \over { \kappa^3 R } } \right ]_{\mbox{ret} }](images/math/9/3/3/933669c2d1a096c8d88f364b5936be13.png)
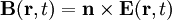
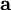 is the acceleration,
is the acceleration,
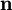 is a unit vector in the
is a unit vector in the 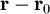 direction,
direction,
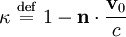
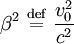
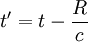 .
.
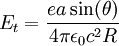 .
.