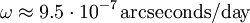To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Thomas precessionIn physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction to the precession of a gyroscope in a rotating non-inertial frame. Product highlight
HistoryThomas precession in relativity was already known to Silberstein[1] in 1914. But the only knowledge Thomas had of relativistic precession came from de Sitters paper on the relativistic precession of the moon, first published in a book by Eddington[2]. In 1925 Thomas relativistically recomputed the precessional frequency of the doublet separation in the fine structure of the atom. He thus found the missing factor 1/2 which came to be known as the Thomas half. This discovery of the relativistic precession of the electron spin led to the understanding of the significance of the relativistic effect. The effect was therefore named Thomas precession PhysicsTo find the Thomas precession we assume the system is in a rotating Minkowski space. The metric in cylindrical coordinates r,φ',z is given by: The frame rotates with a constant angular velocity ω so φ = φ' − ωt and the real metric is given by: This is the so called canonical form of the metric. From this we can read of the relativistic vector potential: We can now calculate the rotational rate of the gyroscope using: In this equation k is the spatial component of the metric. And using the convention rω = v for the velocity we find: So after one revolution the correction to the precession is given by: ApplicationsIn Quantum MechanicsIn quantum mechanics Thomas precession is a correction to the spin-orbit interaction, which takes into account the relativistic time dilation between the electron and the nucleus in hydrogenic atoms. Basically, it states that spinning objects precess when they accelerate in special relativity because Lorentz boosts do not commute with each other. In a Foucault pendulumThomas precession gives a correction to the precession of a Foucault pendulum. For a Foucault pendulum located in the city of Nijmegen in the Netherlands the correction is:
References
Textbooks
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Thomas_precession". A list of authors is available in Wikipedia. |





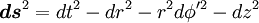
![\boldsymbol{ds}^{2} = (1 - r^{2} \omega^{2}) \left[dt^{2} - 2 dt d\phi \frac{r^{2} \omega}{1 - r^{2} \omega^{2}} + \left(\frac{r^{2} \omega}{1 - r^{2} \omega^{2}}\right)^{2} d\phi^{2}\right] - dr^{2} - \frac{r^{2}}{1 - r^{2} \omega^{2}} d\phi^{2} - dz^{2}](images/math/f/0/d/f0d228590ff784ca88e3ca8209fcf613.png)
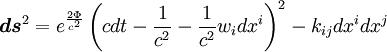
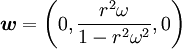
![|\boldsymbol{\Omega}| = \frac{1}{2\sqrt{2}c} e^{\frac{\Phi}{c^{2}}}\left[k^{ik}k^{jl}(w_{i,j} - w_{j,i})(w_{k,l} - w_{l,k})\right]^{1/2}](images/math/1/8/6/186f2a7289048b90503ec7ef17386318.png)
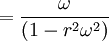
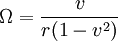
![\alpha = \Omega \Delta \tau - 2\pi = 2\pi \left[\frac{1}{\sqrt{1-v^{2}}} - 1\right] \approx \pi v^{2}](images/math/6/d/3/6d3a8848033285c66b103c9f65f0a385.png)