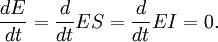To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Competitive inhibitionCompetitive inhibition is a form of enzyme inhibition where binding of the inhibitor to the enzyme prevents binding of the substrate and vice versa. Product highlight
MechanismIn competitive inhibition, the inhibitor binds to the same active site as the normal enzyme substrate, without undergoing a reaction. The substrate molecule cannot enter the active site while the inhibitor is there, and the inhibitor cannot enter the site when the substrate is there. In this case, the maximum speed of the reaction is unchanged, while the apparent affinity of the substrate to the binding site is decreased (it means: the Kd dissociation constant is apparently increased). The change in Km (Michaelis-Menten constant) is parallel to the alteration in Kd. Any given competitive inhibitor concentration can be overcome by increasing the substrate concentration in which case the substrate will outcompete the inhibitor in binding to the enzyme. Note that the inhibitor does not necessarily have to bind to the same active site that the substrate would bind to. As long as the binding of the inhibitor prevents the binding of the substrate (before it has done so), the inhibition mechanism is competitive. This can be observed by the binding of an inhibitor to a secondary site on the enzyme causing a conformational change in the structure such that the substrate cannot bind. EquationVmax remains the same because the presence of the inhibitor can be overcome by higher substrate concentrations. where KI is the inhibitors dissociation constant and [I] is the inhibitor concentration. DerivationIn the simplest case of a single-substrate enzyme obeying Michaelis-Menten kinetics, the typical scheme
is modified to include binding of the inhibitor to the free enzyme:
Note that the inhibitor does not bind to the ES complex and the substrate does not bind to the EI complex. It is generally assumed that this behavior is indicative of both compounds binding at the same site, but that is not strictly necessary. To derive the equation describing the kinetics, first assign microscopic rate constants to each step:
Just as with the derivation of the Michaelis-Menten equation, assume that the system is at steady-state, that is that the concentration of each of the enzyme species is not changing. Furthermore, the known total enzyme concentration is ET = E + ES + EI, the velocity is measured under conditions in which the substrate and inhibitor concentrations do not change substantially and an insignificant amount of product has accumulated. We can therefore set up a system of equations:
where S, I and ET are known. The initial velocity is defined as v = dP/dt = k2 ES, so we need to define the unknown ES in terms of the knowns S, I and ET. From eq 3, we can define E in terms of ES by rearranging to
Dividing by k1 S gives
As in the derivation of the Michaelis-Menten equation, the term (k-1+k2)/k1 can be replaced by the macroscopic rate constant Km:
Substituting eq 5 into eq 4, we have
Rearranging, we find that
At this point, we can define the dissociation constant for the inhibitor as Ki = k−3/k3, giving
At this point, substitute eq 5 and eq 6 into eq 1:
Rearranging to solve for ES, we find
=> eq 7: ES = ET*S*Ki/(Km*Ki+S*Ki+I*Km) Returning to our expression for v, we now have v = k2*ES = k2*ET*S*Ki/(Km*Ki+S*Ki+I*Km) Rearranging and replacing k2 with kcat, we have
Finally, we can replace kcat*ET with Vmax and combine terms to yield the conventional form:
see also
|
|||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Competitive_inhibition". A list of authors is available in Wikipedia. | |||||||





![\text{apparent } K_m=K_m\times \left(1+\frac{[I]}{K_I}\right)](images/math/c/c/b/ccba76c99fee89d0b003398cfda79a3a.png)