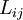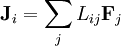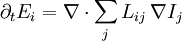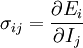To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Onsager reciprocal relationsIn thermodynamics, the Onsager reciprocal relations express the equality of certain relations between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists. As an example, it is observed that temperature differences in a system lead to heat flows from the warmer to the colder parts of the system. Similarly, pressure differences will lead to matter flow from high-pressure to low-pressure regions. It was observed experimentally that when both pressure and temperature vary, pressure differences can cause heat flow and temperature differences can cause matter flow. Even more surprisingly, the heat flow per unit of pressure difference and the density (matter) flow per unit of temperature difference are equal. This was shown to be necessary by Lars Onsager using statistical mechanics. Similar "reciprocal relations" occur between different pairs of forces and flows in a variety of physical systems. The theory developed by Onsager is much more general than this example and capable of treating more than two thermodynamic forces at once. Product highlight
Example: Fluid systemThermodynamic potentials, forces and flowsThe basic thermodynamic potential is internal energy. In a fluid system, the energy density where
The extensive quantities and
where The gradients of the conjugate variables (thermodynamics) of
and, in the absence of heat flows,
where The reciprocity relationsIn this example, when there are both heat and matter flows, there are "cross-terms" in the relationship between flows and forces (the proportionality coefficients are customarily denoted by and
The Onsager reciprocity relations state the equality of the cross-coefficients
Abstract formulationLet where defines the intensive quantity The gradients of the intensive quantities are thermodynamic forces: and they cause fluxes The fluxes are proportional to the thermodynamic forces by a matrix of coefficients Then, Introducing a susceptibility matrix we have Categories: Thermodynamics | Non-equilibrium thermodynamics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Onsager_reciprocal_relations". A list of authors is available in Wikipedia. |





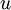 depends on matter density
depends on matter density 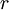 and entropy density
and entropy density 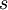 in the following way:
in the following way:
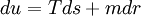
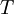 is temperature and
is temperature and 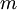 is a combination of pressure and
is a combination of pressure and 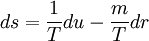 .
.
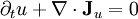
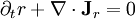 ,
,
 indicates the partial derivative with respect to time
indicates the partial derivative with respect to time 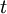 , and
, and 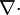 indicates the divergence of the flux densities
indicates the divergence of the flux densities 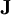 .
.
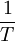 and
and  , are thermodynamic forces and they cause flows of the corresponding extensive variables.
In the absence of matter flows,
, are thermodynamic forces and they cause flows of the corresponding extensive variables.
In the absence of matter flows,
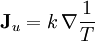 ;
;
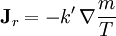 ,
,
 now indicates the gradient.
now indicates the gradient.
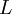 ):
):
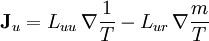
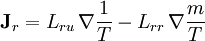 .
.
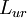 and
and 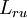 . Proportionality follows from simple dimensional analysis (i.e., both coefficients are measured in the same units of temperature times mass density).
. Proportionality follows from simple dimensional analysis (i.e., both coefficients are measured in the same units of temperature times mass density).
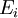 be the extensive variables on which entropy
be the extensive variables on which entropy 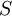 depends. In the following analysis, these symbols will refer to densities of these thermodynamic quantities. Then,
depends. In the following analysis, these symbols will refer to densities of these thermodynamic quantities. Then,
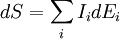
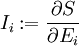
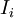 conjugate to the extensive quantity
conjugate to the extensive quantity 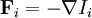
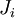 of the extensive quantities satisfying continuity equations
of the extensive quantities satisfying continuity equations