To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Conjugate variables (thermodynamics)
In thermodynamics, the internal energy of a system is expressed in terms of pairs of conjugate variables such as pressure/volume or temperature/entropy. In fact all thermodynamic potentials are expressed in terms of conjugate pairs. For a mechanical system, a small increment of energy is the product of a force times a small displacement. A very similar situation exists in thermodynamics. An increment in the energy of a thermodynamic system can be expressed as the sum of the products of certain generalized "forces" which, when imbalanced cause certain generalized "displacements", and the product of the two is the energy transferred as a result. These forces and their associated displacements are called conjugate variables. The thermodynamic force is always an intensive variable and the displacement is always an extensive variable, yielding an extensive energy transfer. The intensive (force) variable is the derivative of the internal energy with respect to the extensive (displacement) variable, while all other extensive variables are held constant. Product highlight
ExampleFor example, for a system with two types of particles, a small change in the internal energy is given by:
where U is internal energy, T is temperature, S is entropy, P is pressure, V is volume, μi is the chemical potential of the i-th particle type, and Ni is the number of i-type particles in the system. In the above equation, the equal sign holds for a reversible change in the energy. The most commonly considered conjugate thermodynamic variables are (with corresponding SI units):
Here, the pressure, temperature, and chemical potential are the generalized forces, which drive the generalized changes in volume, entropy, and particle number respectively. These parameters all affect the internal energy of a thermodynamic system. In particular we may say that, for reversible processes, the energy balance is expressed as:
where dU is an increment in the internal energy of the system, and the following terms represent the flow of energy across the boundaries of the system due to the corresponding conjugate pair. These concepts will be expanded upon in the following sections. The pressure/volume and stress/strain pairAs an example, consider the PV conjugate pair. The pressure acts as a generalized force - pressure differences force a change in volume, and their product is the energy lost by the system due to mechanical work. Pressure is the driving force, volume is the associated displacement, and the two form a pair of conjugate variables. The above holds true only for non-viscous fluids. In the case of viscous fluids, plastic and elastic solids, the pressure force is generalized to the stress tensor, and changes in volume are generalized to the volume multiplied by the strain tensor (Landau & Lifshitz 1986). These then form a conjugate pair. If σij is the ij component of the stress tensor, and or, using Einstein notation for the tensors, in which repeated indices are assumed to be summed: In the case of pure compression (i.e. no shearing forces), the stress tensor is simply the negative of the pressure times the unit tensor so that The trace of the strain tensor ( The temperature/entropy pairIn a similar way, temperature differences drive changes in entropy, and their product is the energy transferred by heating. We should note that this is the only heat term, the other terms are essentially all various forms of work. The chemical potential/particle number pairThe chemical potential is like a force which pushes an increase in particle number. In cases where there are a mixture of chemicals and phases, this is a useful concept. For example if a container holds water and water vapor, there will be a chemical potential (which is negative) for the liquid pushing water molecules into the vapor (evaporation) and a chemical potential for the vapor, pushing vapor molecules into the liquid (condensation). Only when these "forces" equilibrate is equilibrium obtained. Other conjugate variablesThere are many other types of conjugate variables, depending on the type of work a certain system is doing (or is being subjected to). Notations vary somewhat, but following are common.
See alsoGeneralized coordinates Generalized force References
|
|||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Conjugate_variables_(thermodynamics)". A list of authors is available in Wikipedia. |





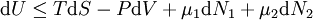 ,
,
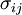 (
(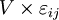 (m3 = J Pa-1)
(m3 = J Pa-1)
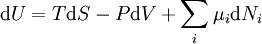 ,
,
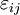 is the ij component of the strain tensor, then the mechanical work done as the result of a stress-induced infinitesimal strain
is the ij component of the strain tensor, then the mechanical work done as the result of a stress-induced infinitesimal strain 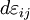 is:
is:
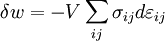
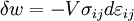
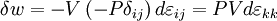
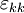 ) is just the fractional change in volume so that the above reduces to
) is just the fractional change in volume so that the above reduces to 

