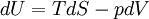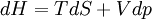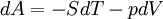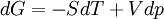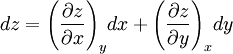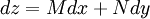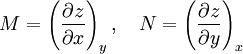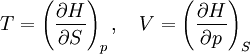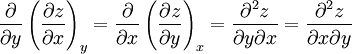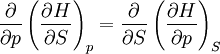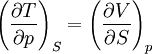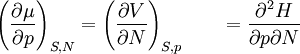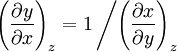To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Maxwell relationsMaxwell's relations are a set of equations in thermodynamics which are derivable from the definitions of the thermodynamic potentials. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of differentiation of an analytic function of two variables is irrelevant. If Φ is a thermodynamic potential and xi and xj are two different natural variables for that potential, then the Maxwell relation for that potential and those variables is: where the partial derivatives are taken with all other natural variables held constant. It is seen that for every thermodynamic potential there are n(n-1)/2 possible Maxwell relations where n is the number of natural variables for that potential. Product highlight
The four most common Maxwell relationsThe four most common Maxwell relations are the equalities of the second derivatives of each of the four thermodynamic potentials, with respect to their thermal natural variable (temperature T or entropy S ) and their mechanical natural variable (pressure p or volume V ): where the potentials as functions of their natural thermal and mechanical variables are:
Derivation of the Maxwell relationsDerivation of the Maxwell equations can be deduced from the differential forms of the thermodynamic potentials: These equations resemble total differentials of the form And indeed, it can be shown that for any equation of the form that Consider, as an example, the equation Since we also know that for functions with continuous second derivatives, the mixed partial derivatives are identical, that is, that we therefore can see that and therefore that Each of the four Maxwell relationships given above follows similarly from one of the Gibbs equations. General Maxwell relationshipsThe above are by no means the only Maxwell relationships. When other work terms involving other natural variables besides the volume work are considered or when the number of particles is included as a natural variable, other Maxwell relations become apparent. For example, if we have a single-component gas, then the number of particles N is also a natural variable of the above four thermodynamic potentials. The Maxwell relationship for the enthalpy with respect to pressure and particle number would then be: where μ is the chemical potential. In addition, there are other thermodynamic potentials besides the four that are commonly used, and each of these potentials will yield a set of Maxwell relations. Each equation can be re-expressed using the relationship which are sometimes also known as Maxwell relations. See also |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Maxwell_relations". A list of authors is available in Wikipedia. |
- Category:Semiconductor_analysis
- Lipinski's_Rule_of_Five
- CSIC presents its prototype vanadium battery for large-scale electrical energy storage - 10 kW redox flow demonstrator paves the way for a 50 kW flow battery
- DNA
- Gold shines through properties of nano biosensors - Fluorescence in ligand-protected gold nanoclusters is an intrinsic property of the gold particles themselves


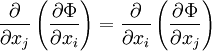



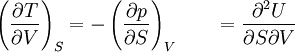
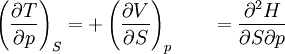
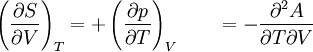
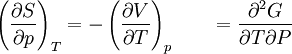
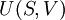 - The
- The 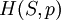 - The
- The 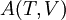 - The
- The 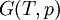 - The
- The