To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Isentropic processIn thermodynamics, an isentropic process (iso = "equal" (Greek); entropy = "disorder") is one during which the entropy of the system remains constant. Product highlight
BackgroundSecond law of thermodynamics states that, where δQ is the amount of energy the system gains by heating, T is the temperature of the system, and dS is the change in entropy. The equal sign will hold for a reversible process. For a reversible isentropic process, there is no transfer of heat energy and therefore the process is also adiabatic. For an irreversible adiabatic process, the entropy will increase. Hence removal of heat from the system (cooling) is necessary to maintain a constant internal entropy for an irreversible process. Thus an irreversible isentropic process is not adiabatic. For reversible processes, an isentropic transformation is carried out by thermally "insulating" the system from its surroundings. Temperature is the thermodynamic conjugate variable to entropy, and so the conjugate process would be an isothermal process in which the system is thermally "connected" to a constant-temperature heat bath. Isentropic flowAn isentropic flow is a flow that is both adiabatic and reversible. That is, no energy is added to the flow, and no energy losses occur due to friction or dissipative effects. For an isentropic flow of a perfect gas, several relations can be derived to define the pressure, density and temperature along a streamline. Derivation of the isentropic relationsFor a closed system, the total change in energy of a system is the sum of the work done and the heat added,
The work done on a system by changing the pressure is,
where p being the pressure and V the specific volume. The change in enthalpy (H = U + pV) is given by,
Since a reversible process is adiabatic (i.e. no heat transfer occurs), so dQ = 0. This leads to two important observations,
The heat capacity ratio can be written as, For an ideal gas γ is constant. Hence on integrating the above equation, we get
Using the equation of state for an ideal gas, pV = RT,
See alsoCategories: Thermodynamic processes | Thermodynamic entropy |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Isentropic_process". A list of authors is available in Wikipedia. |






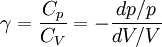
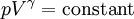 i.e.
i.e.