To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Heat capacity ratio
The heat capacity ratio or adiabatic index, is the ratio of the heat capacity at constant pressure (CP) to heat capacity at constant volume (CV). It is sometimes also known as the isentropic expansion factor and ratio of specific heats, and is denoted by γ (gamma) or κ (kappa). The latter symbol kappa is primarily used by chemical engineers. where, C is the heat capacity or the specific heat capacity of a gas, suffix P and V refer to constant pressure and constant volume conditions respectively. To understand this relation, consider the following experiment: A closed cylinder with a locked piston contains air. The pressure inside is equal to the outside air pressure. This cylinder is heated. Since the piston cannot move the volume is constant. Temperature and pressure rise. Heating is stopped and the energy added to the system, which is proportional to CV, is noted. The piston is now freed and moves outwards, expanding without exchange of heat (adiabatic expansion). Doing this work (proportional to CP) cools the air inside the cylinder to below its starting temperature. To return to the starting temperature (still with a free piston) the air must be heated. This extra heat amounts to about 40% of the previous amount added. In the preceding, it may not be obvious how CP is involved because during the expansion and subsequent heating, the pressure does not remain constant. Another way of understanding the difference between CP and CV is to consider the difference between adding heat to the gas with a locked piston, and adding heat with a piston free to move, so that pressure remains constant. In that case, the gas will both heat and expand, causing the piston to do mechanical work on the atmosphere. The heat that is added to the gas goes only partly into heating the gas; while the rest is transformed into the mechanical work performed by the piston. In the constant-volume case (locked piston) there is no external motion, and thus no mechanical work is done on the atmosphere. Thus the amount of heat required to raise the gas temperature (the heat capacity) is higher in the constant pressure case. Product highlight
Ideal gas relationsFor an ideal gas, the heat capacity is constant with temperature. Accordingly we can express the enthalpy as H = CPT and the internal energy as U = CVT. Thus, it can also be said that the heat capacity ratio is the ratio between the enthalpy to the internal energy: Furthermore, the heat capacities can be expressed in terms of heat capacity ratio ( γ ) and the gas constant ( R ): It can be rather difficult to find tabulated information for CV, since CP is more commonly tabulated. The following relation, can be used to determine CV:
Relation with degrees of freedomThe heat capacity ratio ( γ ) for an ideal gas can be related to the degrees of freedom ( f ) of a molecule by: Thus we observe that for a monatomic gas, with three degrees of freedom:
while for a diatomic gas, with five degrees of freedom (at room temperature):
E.g.: The terrestrial air is primarily made up of diatomic gasses (~78% nitrogen (N2) and ~21% oxygen (O2)) and, at standard conditions it can be considered to be an ideal gas. A diatomic molecule has five degrees of freedom (three translational and two rotational degrees of freedom, the vibrational degree of freedom is not involved except at high temperatures). This results in a value of
This is consistent with the measured adiabatic index of approximately 1.403 (listed above in the table). Real gas relationsAs temperature increases, higher energy rotational and vibrational states become accessible to molecular gases, thus increasing the number of degrees of freedom and lowering γ. For a real gas, CP and CV usually increase with increasing temperature and γ decreases. Some correlations exist to provide values of γ as a function of the temperature. Adiabatic processThis ratio also gives the important relation for a quasistatic, adiabatic process: where, p is the pressure and V is the volume. The subscripts 1 and 2 refer to conditions before and after the process, or at any time during that process. See also
References
Categories: Heat | Heat transfer |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Heat_capacity_ratio". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


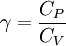



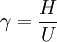
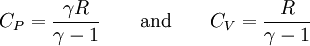
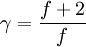
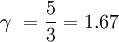 ,
,
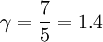 .
.
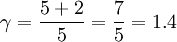 .
.