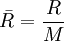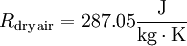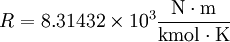To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Gas constant
The gas constant (also known as the universal or ideal gas constant, usually denoted by symbol R) is a physical constant which features in large number of fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy per kelvin per mole (rather than energy per kelvin per particle). Its value is:
The two digits in parentheses are the uncertainty (standard deviation) in the last two digits of the value. The gas constant occurs in the simplest equation of state, the ideal gas law, as follows: where
Product highlight
Relationship with the Boltzmann constantThe Boltzmann constant kB (often abbreviated k) may be used in place of the gas constant by working in pure particle count, N, rather than number of moles, n, since R = NAkB, where NA is Avogadro's number. For example, the ideal gas law in terms of Boltzmann's constant is: Specific gas constantThe specific gas constant of a gas or a mixture of gases ( It is common to represent the specific gas constant by the symbol R. In such cases the context and/or units of R should make it clear as to which gas constant is being referred to. For example, the equation for the speed of sound is usually written in terms of the specific gas constant. The specific gas constant of dry air is US Standard AtmosphereThe US Standard Atmosphere, 1976 (USSA1976) defines the Universal Gas Constant as:[1][2] The USSA1976 does recognize, however, that this value is not consistent with the cited values for the Avogadro constant and the Boltzmann constant.[2] This disparity is not a significant departure from accuracy, and USSA1976 uses this value of R for all the calculations of the standard atmosphere. When using the ISO value of R, the calculated pressure increases by only 0.62 pascals at 11,000 meters (the equivalent of a difference of only 0.174 meters – or 6.8 inches) and an increase of 0.292 pascals at 20,000 meters (the equivalent of a difference of only 0.338 meters – or 13.2 inches). See alsoReferences |
|||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gas_constant". A list of authors is available in Wikipedia. |


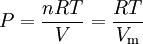



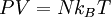
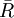 ) is given by the universal gas constant, divided by the
) is given by the universal gas constant, divided by the