To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Avogadro constantThe Avogadro constant (symbols: L, NA), also called the Avogadro number is the number of "entities" (usually, atoms or molecules) in one mole,[1][2] that is the number of carbon-12 atoms in 12 grams (0.012 kg) of unbound carbon-12 in its ground state. The current best estimate of this number is: [3] The value of the number was first indicated by Johann Josef Loschmidt, who in 1865, computed the number of particles in one cubic centimetre of gas in standard conditions. The term Loschmidt constant is thus more correctly applied for this latter value, which can be said to be proportional to the Avogadro number. However, in German language literature, "Loschmidt constant" is used to refer to both this usage, as well as the number of entities in a mole. Product highlight
History and etymologyThe Avogadro constant is named after the early nineteenth century Italian scientist Amedeo Avogadro, who is credited (1811) with being the first to realize that the volume of a gas (strictly, of an ideal gas) is proportional to the number of atoms or molecules. The French chemist Jean Baptiste Perrin in 1909 proposed naming the constant in honor of Avogadro. American chemistry textbooks picked it up in the 1930s followed by high school textbooks starting in the 1950s.[4] Loschmidt: Measuring the Avogadro NumberAvogadro never attempted to measure the constant: the numerical value was first estimated by the Austrian physicist Johann Josef Loschmidt in 1865 using the kinetic theory of gases.[5] In German-speaking countries, the constant is sometimes referred to as the Loschmidt constant or Loschmidt's number, but what Loschmidt actually measured is the number of particles per unit volume of an ideal gas, i.e. the number density of particles in an ideal gas. Thus, the term Loschmidt constant is more appropriate to the number of particles per unit of gas, Symbol: no:[6] equal to (2.686 7774 ± 0.000 0047) × 1025 m−3 at 273.15 K and 101.325 kPa with kB the Boltzmann constant, T the temperature and p the pressure. This constant is related to the Avogadro constant by the relation: with kB the Boltzmann constant hence However, in German scientific literature, the term Loschmidt constant is used ambiguously - it often refers to what has come to be known as Avogadro number.[7] However, Boltzmann had first used the term for the sense in which Loschmidt had measured it - the number of particles in an unit volume of gas. Thus, its use in referring to the related Avogadro number leads to confusion and is usually deprecated. For the same reason, sometimes the Avogadro Number is denoted as L as opposed to NA in German texts.[5] Standardization of the moleBefore 1960, there were conflicting definitions of the mole, and hence of the Avogadro number (as it was known at the time), based on 16 grams of oxygen: physicists generally used oxygen-16 while chemists generally used the "naturally occurring" isotope ratio. Switching to 12 grams of carbon-12 as the basis ended this dispute and had other advantages.[8] At this time, the Avogadro number was defined as the number of atoms in 12 grams of carbon-12, that is as a dimensionless quantity, while a mole was defined as one Avogadro number of atoms, molecules or other entities. When the mole entered the International System of Units (SI) in 1971 as the base unit of amount of substance, the definitions were interchanged: what had previously been a number became a physical constant with the unit of reciprocal moles (mol−1). ApplicationThe Avogadro constant can be applied to any substance. It corresponds to the number of atoms or molecules needed to make up a mass equal to the substance's atomic or molecular mass, in grams. For example, the atomic mass of iron is 55.847 g/mol, so NA iron atoms (i.e. one mole of iron atoms) have a mass of 55.847 g. Conversely, 55.847 g of iron contains NA iron atoms. The Avogadro constant also enters into the definition of the unified atomic mass unit, u: Additional physical relationsBecause of its role as a scaling factor, the Avogadro number provides the link between a number of useful physical constants when moving between the atomic scale and the macroscopic scale. For example, it provides the relationship between:
Measurement of the Avogadro constantA number of methods can be used to measure the Avogadro constant. One modern method is to calculate the Avogadro constant from the density (ρ) of a crystal, the relative atomic mass (M), and the unit cell length (a) determined from x-ray crystallography.[9] Very accurate values of these quantities for silicon have been measured at the National Institute of Standards and Technology (NIST) and used to obtain the value of the Avogadro constant:
See also
References and notes
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Avogadro_constant". A list of authors is available in Wikipedia. |


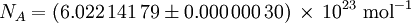



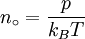
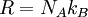
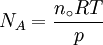
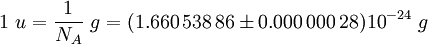
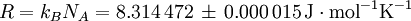
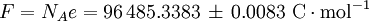
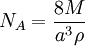 .
.


