To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Molar massMolar mass, symbol M,[1] is the mass of one mole of a substance (chemical element or chemical compound).[2] It is a physical property which is characteristic of each pure substance. The base SI unit for mass is the kilogram[1] but, for both practical and historical reasons, molar masses are almost always quoted in grams per mole (g/mol or g mol–1), especially in chemistry. Molar mass is closely related to the formula weight (F.W.) or relative molar mass (Mr) of a compound, and to the relative atomic masses or the standard atomic weights of its constituent elements. However, it should be distinguished from the molecular mass , which is the mass of one molecule (of any single isotopic composition) and is not directly related to the atomic mass, the mass of one atom (of any single isotope). The dalton, symbol Da, is also sometimes used as a unit of molar mass, especially in biochemistry, with the definition 1 Da = 1 g/mol, despite the fact that it is strictly a unit of molecular mass (1 Da = 1.660 538 782(83)×10–27 kg).[3][4] Molar masses are almost never measured directly. They may be calculated from standard atomic weights, and are often listed in chemical catalogues and on material safety data sheets (MSDS). Molar masses typically vary between:
Product highlight
Molar masses of elementsThe molar mass of atoms of an element is given by the standard atomic weight of the element[5] multiplied by the molar mass constant, Mu = 1×10–3 kg/mol = 1 g/mol:[6]
Multiplying by the molar mass constant ensures that the calculation is dimensionally correct: atomic weights are dimensionless quantities (ie, pure numbers) whereas molar masses have units (in this case, g/mol). Some elements are usually encountered as molecules, eg hydrogen (H2), sulfur (S8), chlorine (Cl2). The molar mass of molecules of these elements is the molar mass of the atoms multiplied by the number of atoms in each molecule:
Molar masses of compoundsThe molar mass of a compound is given by the sum of the standard atomic weights of the atoms which form the compound multiplied by the molar mass constant, Mu:
An average molar mass may be defined for mixtures of compounds.[1] This is particularly important in polymer science, where different polymer molecules may contain different numbers of monomer units (non-uniform polymers).[7] Related propertiesMolecular weight (M.W.) and formula weight (F.W.) are older terms for what is now more correctly called the relative molar mass (Mr).[2] This is a dimensionless quantity (ie, a pure number, without units) equal to the molar mass divided by the molar mass constant.[8] Molecular massThe molecular mass (m) is the mass of a given molecule: it is measured in daltons (Da) or atomic mass units (u), where 1 Da = 1 u = 1.660 538 782(83)×10–27 kg).[3][4] Different molecules of the same compound may have different molecular masses because they contain different isotopes of an element. The molar mass is a measure of the average molecular mass of all the molecules in a sample, and is usually the more appropriate measure when dealing with macroscopic (weighable) quantities of a substance. Molecular masses are calculated from the relative atomic masses[9] of each nuclide, while molar masses are calculated from the atomic weights of each element. The atomic weight takes into account the isotopic distribution of the element in a given sample (usually assumed to be "normal"). For example, water has a molar mass of 18.0153(3) g/mol, but individual water molecules have molecular masses which range between 18.010 564 6863(15) u (1H216O) and 22.027 7364(9) u (2H218O). The distinction between molar mass and molecular mass is important because relative molecular masses can be measured directly by mass spectrometry, often to a precision of a few parts per million. This is accurate enough to directly determine the chemical formula of a molecule.[10] Precision and uncertaintiesThe precision to which a molar mass is known depends on the precision of the atomic weights from which it was calculated. Most atomic weights are known to a precision of at least one part in ten-thousand, often much better[5] (the atomic weight of lithium is a notable, and serious,[11] exception). This is adequate for almost all normal uses in chemistry: it is more precise than most chemical analyses, and exceeds the purity of most laboratory reagents. The precision of atomics weights, and hence of molar masses, is limited by the knowledge of the isotopic distribution of the element. If a more accurate value of the molar mass is required, it is necessary to determine the isotopic distribution of the sample in question, which may be different from the standard distribution used to calculate the standard atomic weight. The isotopic distributions of the different elements in a sample are not necessarily independent of one another: for example, a sample which has been distilled will be enriched in the lighter isotopes of all the elements present. This complicates the calculation of the standard uncertainty in the molar mass. A useful convention for normal laboratory work is to quote molar masses to two decimal places for all calculations. This is more accurate than is usually required, but avoids rounding errors during calculations. When the molar mass is greater than 1000 g/mol, it is rarely appropriate to use more than one decimal place. These conventions are followed in most tabulated values of molar masses.[12] MeasurementWhile molar masses are almost always, in practice, calculated from atomic weights, they can also be measured in certain cases. Such measurements are much less precise than modern mass spectrometric measurements of atomic weights and molecular masses, and are of mostly historical interest. All of the procedures rely on colligative properties, and any dissociation of the compound must be taken into account. Vapour densityThe measurement of molar mass by vapour density relies on the principle, first enounced by Amadeo Avogadro, that equal volumes of gases under identical conditions contain equal numbers of particles. This principle is included in the ideal gas equation:
where n is the amount of substance. The vapour density (ρ) is given by
Combining these two equations gives an expression for the molar mass in terms of the vapour density for conditions of known pressure and temperature. Freezing-point depressionThe freezing point of a solution is lower than that of the pure solvent, and the freezing-point depression (ΔT) is directly proportional to the amount concentration for dilute solutions. When the amount concentration is expressed as a molality, the proportionality constant is known as the cryoscopic constant (Kf) and is characteristic for each solvent. If w represents the mass fraction of the solute in solution, and assuming no dissociation of the solute, the molar mass is given by
Boiling-point elevationThe boiling point of a solution of an involatile solute is higher than that of the pure solvent, and the boiling-point elevation (ΔT) is directly proportional to the amount concentration for dilute solutions. When the amount concentration is expressed as a molality, the proportionality constant is known as the ebullioscopic constant (Kb) and is characteristic for each solvent. If w represents the mass fraction of the solute in solution, and assuming no dissociation of the solute, the molar mass is given by
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Molar_mass". A list of authors is available in Wikipedia. |





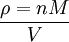 .
.
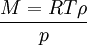
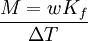 .
.
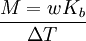 .
.


