To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Nernst equationIn electrochemistry, the Nernst equation is used to calculate equilibrium reduction potential (electromotive force), E, of an electrochemical cell (or half-cell) from its standard reduction potential (or standard electrode potential), E0, and the activities (effective concentrations) of its components. It is named after the German physical chemist who first formulated it, Walther Nernst. It is used in physiology for finding the electric potential of a cell membrane with respect to one type of ion. where
The constant RT/F may be replaced by 25.679 mV for cells at room temperature (25 °C). The Nernst equation is frequently expressed in terms of base 10 logarithms rather than natural logarithms, in which case it is written, for a cell at 25 °C:
Note that the Nernst equation is expressed more generally by replacing the ratio of activities with the reaction quotient Q. Product highlight
Physiological application: the Nernst potentialFor a cell membrane potential with respect to one cation, (the sign before the logarithm changes to a minus for anions). The potential level across the cell membrane that exactly opposes net diffusion of a particular ion through the membrane is called the Nernst potential for that ion. As seen above, the magnitude of the Nernst potential is determined by the ratio of the concentrations of that specific ion on the two sides of the membrane. The greater this ratio, the greater the tendency for the ion to diffuse in one direction, and therefore the greater the Nernst potential required to prevent the diffusion. Derivation
The Nernst Equation may be derived in several different ways. Chemistry textbooks frequently give the derivation in terms of entropy and the Gibbs free energy, but there is a more intuitive method for anyone familiar with Boltzmann factors. Using Boltzmann factorsFor simplicity, we will consider a solution of redox-active molecules that undergo a one electron reversible reaction and which have a standard potential of zero. The chemical potential μc of this solution is the difference between the energy barriers for taking electrons from and for giving electrons to the working electrode that is setting the solution's electrochemical potential. The ratio of oxidized to reduced molecules, [Ox]/[Red], is equivalent to the probability of being oxidized (giving electrons) over the probability of being reduced (taking electrons), which we can write in terms of the Boltzmann factors for these processes: Taking the natural logarithm of both sides gives If Dividing the equation by e to convert from chemical potentials to electrode potentials, and remembering that kT/e = RT/F, we obtain the Nernst equation for the one-electron process
Using entropy and Gibbs free energyQuantities here are given per molecule, not per mole, and so Boltzmann's constant k and the electron charge e are used instead of the gas constant R and Faraday's constant F. To convert to the molar quantities given in most chemistry textbooks, it is simply necessary to multiply by Avogadro's number: R = kNA and F = eNA. The entropy of a molecule is defined as where Ω is the number of states available to the molecule. The number of states must vary linearly with the volume V of the system, which is inversely proportional to the concentration c, so we can also write the entropy as The change in entropy from some state 1 to another state 2 is therefore so that the entropy of state 1 is If state 1 is at standard conditions, in which c1 is unity (e.g., 1 atm or 1 M), it will merely cancel the units of c2. We can therefore write the entropy of an arbitrary molecule A as where S0 is the entropy at standard conditions and [A] denotes the concentration of A. The change in entropy for a reaction is then given by We define the ratio in the last term as the reaction quotient: In an electrochemical cell, the cell potential E is the chemical potential available from redox reactions (E = μc / e). E is related to the Gibbs free energy change ΔG only by a constant: ΔG = − neE, where n is the number of electrons transferred. (There is a negative sign because a spontaneous reaction has a negative ΔG and a positive E.) The Gibbs free energy is related to the entropy by G = H − TS, where H is the enthalpy and T is the temperature of the system. Using these relations, we can now write the change in Gibbs free energy, and the cell potential, This is the more general form of the Nernst equation.
For the redox reaction
The cell potential at standard conditions E0 is often replaced by the formal potential E0', which includes some small corrections to the logarithm and is the potential that is actually measured in an electrochemical cell. LimitationsIn dilute solutions, the Nernst equation can be expressed directly in terms of concentrations (since activity coefficients are close to unity). But at higher concentrations, the true activities of the ions must be used. This complicates the use of the Nernst equation, since estimation of non-ideal activities of ions generally requires experimental measurements. The Nernst equation also only applies when there is no net current flow through the electrode. The activity of ions at the electrode surface changes when there is current flow, and there are additional overpotential and resistive loss terms which contribute to the measured potential. See also |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Nernst_equation". A list of authors is available in Wikipedia. |


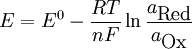
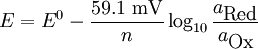 .
.



![E = E^0 + \frac{59.1\mbox{ mV}}{n} \log_{10}\frac{\gamma_{\mbox{outside}}[\mbox{ion outside cell}]}{\gamma_{\mbox{inside}}[\mbox{ion inside cell}]}](images/math/8/a/6/8a679cfd2459e3c083d2093e729b2bee.png)
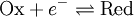
![\frac{[\mathrm{Ox}]}{[\mathrm{Red}]} = \frac{\exp \left(-[\mbox{barrier for losing an electron}]/kT\right)} {\exp \left(-[\mbox{barrier for gaining an electron}]/kT\right)} = \exp \left(\mu_c / kT \right).](images/math/c/c/e/cced0eb2349e0406bfdbd755b1605c1a.png)
![\mu_c = kT \ln \frac{[\mathrm{Ox}]}{[\mathrm{Red}]}.](images/math/f/f/5/ff5f0da2623e3f6c10e3e28de6c1bdd6.png)
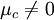 at [Ox]/[Red] = 1, we need to add in this additional
constant:
at [Ox]/[Red] = 1, we need to add in this additional
constant:
![\mu_c = \mu_c^0 + kT \ln \frac{[\mathrm{Ox}]}{[\mathrm{Red}]}.](images/math/f/6/4/f64007dc5d671977fa1118f048af0eba.png)
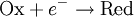 :
:
![E = E^0 + \frac{kT}{e} \ln \frac{[\mathrm{Ox}]}{[\mathrm{Red}]} = E^0 - \frac{RT}{F} \ln \frac{[\mathrm{Red}]}{[\mathrm{Ox}]}.](images/math/a/d/a/ada2c10e0b4876c9638e92e8d7515e16.png)
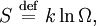
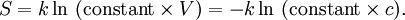
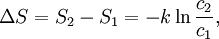
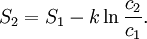
![S(A) = S^0(A) - k \ln [A], \,](images/math/9/8/a/98a583e9be5c433e5c18c8a8bca71688.png)
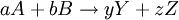
![\Delta S_\mathrm{rxn} = [yS(Y) + zS(Z)] - [aS(A) - bS(B)] = \Delta S^0_\mathrm{rxn} - k \ln \frac{[Y]^y [Z]^z}{[A]^a [B]^b}.](images/math/7/3/7/737e019ac9707b17c118693d5e50ca2a.png)
![Q \ \stackrel{\mathrm{def}}{=}\ \frac{[Y]^y [Z]^z}{[A]^a [B]^b}.](images/math/d/b/f/dbfa2fbb9733ea292f27ed6d5ccb94a3.png)
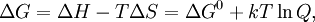
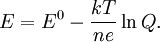
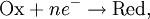
![E = E^0 - \frac{kT}{ne} \ln \frac{[\mathrm{Red}]}{[\mathrm{Ox}]} = E^0 - \frac{RT}{nF} \ln \frac{[\mathrm{Red}]}{[\mathrm{Ox}]}.](images/math/b/a/b/bab984712aba3bd27104b759581a3091.png)


