To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Membrane potential
Membrane potential (or transmembrane potential or transmembrane potential difference or transmembrane potential gradient), is the electrical potential difference (voltage) across a cell's plasma membrane. The plasma membrane bounds the cell to provide a stable environment for biological processes. Membrane potential arises from the action of ion transporters embedded in the membrane which maintain viable ion concentrations inside the cell. The term "membrane potential" is sometimes used interchangeably with cell potential but is applicable to any lipid bilayer or membrane. The membrane potential of most cells is kept relatively stable. Unlike most cells, neurons are specialized to use changes in membrane potential for fast communication, primarily with other neurons. When a neuron fires, the action potential travels down the axon to the synapses: the magnitude of the axonal membrane potential varies dynamically along its length. On reaching a (chemical) synapse, a neurotransmitter is released causing a localized change in potential in the membrane of the target neuron by opening ion channels in its membrane. Product highlight
Graded membrane potentialA graded membrane potential is a gradient of transmembrane potential difference along a length of cell membrane. Graded potentials are particularly important in neurons that lack action potentials, such as some types of retinal neurons. Graded potentials that depolarize the membrane, increasing the membrane potential above the resting potential are important as "triggering potentials" that can spread along the surface of neuronal cell bodies to axon initial segments and trigger action potentials. Graded potentials that hyperpolarize the membrane potential to values more negative than the resting potential can inhibit the generation of action potentials. Graded potentials can arise at either portions of cells that function as sensory receptors or at synapses that are activated by neurotransmitters. These two types of graded potentials are called receptor potentials or synaptic potentials. Graded potentials are distinct from action potentials in that graded potentials spread electric potential changes along cell membranes without activating the kind of constant magnitude propagating signal that is characteristic of the action potential. Graded potentials are highest at a source and decay with increasing distance from the source.Membrane potential is significantly important as far as normal body functions are to be maintained The Ionic Basis of the resting potentialAt its core, the origin of every resting membrane potential is some sort of ion pump exchanger or transporter. Any voltage — membrane potentials included — is a separation of electric charges across a resistive barrier. The typical membrane potential of a cell arises from the separation of sodium ions from intracellular immobile anions across the membrane of the cell. In order for this separation to occur, a concentration gradient of potassium ions must first be set up. This work is done by the ion pumps/transporters and/or exchangers and generally is powered by ATP. In the case of the standard membrane potential across a cell's plasma membrane, potassium (and sodium) gradients are established by the NaKATPase (sodium potassium exchanger). In other cases for example, a membrane potential may be established by acidification of the inside of a membranous compartment (such as the proton pump that generates membrane potential across synaptic vesicle membranes). In its most simple terms one can trace the origin of the energy of the membrane potential (voltage is, after all, potential energy) thus: Solar energy → converted to sugar by plants → converted by glycolysis to ATP → converted to concentration gradient by NaKATPase (sodium/potassium pump) → converted to voltage by passive K+ transport across a selectively permeable cell membrane. ElectroneutralityIn most quantitative treatments of membrane potential, such as the derivation of Goldman equation, electroneutrality is assumed; that is, that there is no measurable charge excess in any side of the membrane. So, although there is an electric potential across the membrane due to charge separation, there is no actual measurable difference in the global concentration of positive and negative ions across the membrane (as it is estimated below), that is, there is no actual measurable charge excess in either side. That occurs because the effect of charge on electrochemical potential is hugely greater than the effect of concentration so an undetectable change in concentration creates a great change on electric potential. Generation of the resting potentialCell membranes are typically permeable to only a subset of ionic species. These species usually include potassium ions, chloride ions, bicarbonate ions, and others. To simplify the description of the ionic basis of the resting membrane potential, it is most useful to consider only one ionic species at first, and consider the others later. Since trans-plasma-membrane potentials are almost always determined primarily by potassium permeability, that is where to start.
The number of ions involved in generating the upstroke of the action potentialYou may have noticed that in the diagram above, while the red arrow (with length proportional to the voltage) was growing, the green arrow (with length proportional to the concentration gradient) was not changing significantly. How can this be? If K+ is leaving the cell, won't this deplete the cell of intracellular K+, thus decreasing the concentration gradient? The answer to the latter question is "not much", the concentration gradient is not dissipated very much. So how can this be? To answer this question, one must understand is that the number of potassium ions that must cross the membrane is actually quite small. This is because the membrane potential occurs only right next to the membrane. The membrane potential is stored in the membrane capacitance, which physically is only the charges in direct contact with the membrane surfaces. The voltage across the capacitor is the membrane potential (see action potential for an example of a membrane RC circuit). Knowing that, one needs only to calculate how much current needs to flow to discharge the membrane capacitance to calculate the number of charges that must flow across the membrane to change the capacitor voltage (membrane potential) by, say 100 mV. The capacitative current that flows into or out of a capacitor to effect a change in membrane potential of amplitude dV, is given by the equation:
This equals 3.3 nanoamps. Now, we wanted to know the number of ions, n, this corresponds to. dt is 2 ms, every ion has 1 elementary charge, e, each, and one coulomb is 6.24×1018 e. Therefore, it would take the movement of 41 million charges (i.e. sodium ions) across the membrane to change the voltage of the cardiomyocyte by 100 mV in 2 ms. We want to know what that will do to the intracellular sodium concentration, which in cardiomyocytes is about 15 millimoles per liter. Avogadro's number, which relates numbers to moles, is 6.022·1023 mol-1: Since the normal inside concentration of sodium is some 15 mM, 8.7 μM entering the cell during the action potential upstroke is only about 0.058% extra sodium ions The bottom line for those who don’t want to sift through the calculation is that only about 40,000,000 sodium ions must cross the membrane to move the membrane potential by 100 mV in 2 ms, and that this constitutes only some 0.06% of the sodium already present in the cell. This is at the action potential's most extreme and in a very large cell. In other cells, calculations may look different, depending on surface-to-volume ratio, max dV/dt etc. Equilibrium potentialsAn equilibrium potential (also called reversal potential or Nernst Potential) is the membrane voltage at which the distribution across the membrane of a particular ion is in equilibrium. This means that the transmembrane voltage exactly matches (resists) the diffusive tendency of the ion (or vice versa), such that the net current of the ion across the membrane is zero and unchanging. The equilibrium potential of a particular ion is designated by the notation Eion. In the previous section, the equilibrium potential specifically for potassium ions was described, but any ion present will have an equilibrium potential that is determined by the concentration difference for that ion across the membrane and temperature. For potassium, EK is typically around −80 mV. For sodium, ENa is typically around +60 mV. Note that the sign of ENa and EK are opposite. This is because the concentration gradient for potassium is directed out of the cell, while the concentration gradient for sodium is directed into the cell. Resting potential revisitedThe resting potential of a cell can be most thoroughly understood by thinking of it in terms of equilibrium potentials. In the example diagram above, the model cell was given only one permeant ion (potassium). In this case, the resting potential of this cell would be the same as the equilibrium potential for potassium. However, a real cell is more complicated, having permeabilities to many ions, each of which contributes to the resting potential. To understand better, consider a cell with only two permeant ions, potassium and sodium. Consider a case where these two ions have equal concentration gradients directed in opposite directions, and that the membrane permeabilities to both ions are equal. K+ leaving the cell will tend to drag the membrane potential toward EK. Na+ entering the cell will tend to drag the membrane potential toward ENa. Since the permeabilities to both ions were set to be equal, the membrane potential will, at the end of the Na/K tug-of-war, end up halfway between ENa and EK. As ENa and EK were equal but of opposite signs, halfway in between is zero, meaning that the membrane will rest at 0 mV. Note that even though the membrane potential at 0 mV is stable, it is not an equilibrium condition because neither of the contributing ions are in equilibrium. Ions diffuse down their electrochemical gradients through ion channels, but the membrane potential is upheld by continual K influx and Na efflux via ion pumps. Closer to the actual case for a real resting potential is that neither the equilibrium potentials nor the permeabilities of Na and K are equal. Na permeability is rather about 5% of the K permeability, whereas EK is about -80 mV and ENa about + 60 mV. Thus the membrane potential will not be right at EK, but rather depolarized from EK by an amount of approximately 5% of the 140 mV difference between EK and ENa. Thus, the cell's resting potential will be about −73 mV. In a more formal notation, the membrane potential is the weighted average of each contributing ion's equilibrium potential. The size of each weight is the relative permeability of each ion. In the normal case, where three ions contribute to the membrane potential:
where
All other values of membrane potentialFrom the viewpoint of biophysics, there is nothing particularly special about the resting membrane potential. It is merely the membrane potential that results from the membrane permeabilities that predominate when the cell is resting. The above equation of weighted averages always applies, but the following approach may be easier to visualize. At any given moment, there are two factors for an ion that determine how much influence that ion will have over the membrane potential of a cell.
Intuitively, this is easy to understand. If the driving force is high, then the ion is being "pushed" across the membrane hard (more correctly stated: it is diffusing in one direction faster than the other). If the permeability is high, it will be easier for the ion to diffuse across the membrane. But what are 'driving force' and 'permeability'?
So in a resting membrane, while the driving force for potassium is low, its permeability is very high. Sodium has a huge driving force, but almost no resting permeability. In this case, the math tells us that potassium carries about 20 times more current than sodium, and thus has 20 times more influence over Em than does sodium. However, consider another case—the peak of the action potential. Here permeability to Na is high and K permeability is relatively low. Thus the membrane moves to near ENa and far from EK. The more ions are permeant, the more complicated it becomes to predict the membrane potential. However, this can be done using the Goldman-Hodgkin-Katz equation or the weighted means equation. By simply plugging in the concentration gradients and the permeabilities of the ions at any instant in time, one can determine the membrane potential at that moment. What the GHK equations says, basically, is that at any time, the value of the membrane potential will be a weighted average of the equilibrium potentials of all permeant ions. The "weighting" is the ions relative permeability across the membrane. Effects and implicationsWhile cells expend energy to transport ions and establish a transmembrane potential, they use this potential in turn to transport other ions and metabolites such as sugar. The transmembrane potential of the mitochondria drives the production of ATP, which is the common currency of biological energy. Cells may draw on the energy they store in the resting potential to drive action potentials or other forms of excitation. These changes in the membrane potential enable communication with other cells (as with action potentials) or initiate changes inside the cell, which happens in an egg when it is fertilized by a sperm. In neuronal cells, an action potential begins with a rush of sodium ions into the cell through sodium channels, resulting in depolarization, while recovery involves an outward rush of potassium through potassium channels. Both these fluxes occur by passive diffusion. See also
References
Categories: Electrochemistry | Electrophysiology | Cell signaling | Signal transduction |
|||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Membrane_potential". A list of authors is available in Wikipedia. |





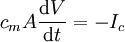
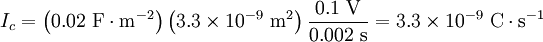
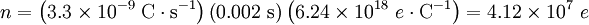
![\Delta [\mbox{Na} ^+]_{ \mbox{i}} = \frac{4.12 \times 10^7 \ e} {\left(6.022 \times 10^{23} \ e \cdot \mathrm{mol}^{-1} \right) \left( 7.85 \times 10^{-12} \ \mathrm{L} \right)} = 8.71 \times 10^{-6} \ \mathrm{mol \cdot L}^{-1}](images/math/d/8/0/d80b06d8cfdcf5c5ae3ea8f03ab80a72.png)
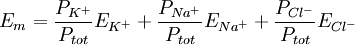 ,
,


