To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Goldman equationThe Goldman-Hodgkin-Katz voltage equation, more commonly known as the Goldman equation is used in cell membrane physiology to determine the potential across a cell's membrane taking into account all of the ions that are permeant through that membrane. Product highlightThe discoverers of this are David E. Goldman of Columbia University, and the English Nobel laureates Alan Lloyd Hodgkin and Bernard Katz. The equationThe GHK voltage equation for N monovalent positive ionic species and M negative: This results in the following if we consider a membrane separating two KxNa1 − xCl-solutions: It is "Nernst-like" but has a term for each permeant ion. The Nernst equation can be considered a special case of the Goldman equation for only one ion:
The first term, before the parenthesis, can be reduced to 61.5 log for calculations at human body temperature (37 C) Note that the ionic charge determines the sign of the membrane potential contribution. The usefulness of the GHK equation to electrophysiologists is that it allows one to calculate the predicted membrane potential for any set of specified permeabilities. For example, if one wanted to calculate the resting potential of a cell, they would use the values of ion permeability that are present at rest (e.g. See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Goldman_equation". A list of authors is available in Wikipedia. |





![E_{m} = \frac{RT}{F} \ln{ \left( \frac{ \sum_{i}^{N} P_{M^{+}_{i}}[M^{+}_{i}]_{out} + \sum_{j}^{M} P_{A^{-}_{j}}[A^{-}_{j}]_{in}}{ \sum_{i}^{N} P_{M^{+}_{i}}[M^{+}_{i}]_{in} + \sum_{j}^{M} P_{A^{-}_{j}}[A^{-}_{j}]_{out}} \right) }](images/math/c/1/b/c1b5c1cf3dbccab5482625658b15f1c2.png)
![E_{m, K_{x}Na_{1-x}Cl } = \frac{RT}{F} \ln{ \left( \frac{ P_{Na^{+}}[Na^{+}]_{out} + P_{K^{+}}[K^{+}]_{out} + P_{Cl^{-}}[Cl^{-}]_{in} }{ P_{Na^{+}}[Na^{+}]_{in} + P_{K^{+}}[K^{+}]_{in} + P_{Cl^{-}}[Cl^{-}]_{out} } \right) }](images/math/8/5/1/851aa82025472a62b619ccb167f5c0a6.png)
![E_{m,Na} = \frac{RT}{F} \ln{ \left( \frac{ P_{Na^{+}}[Na^{+}]_{out}}{ P_{Na^{+}}[Na^{+}]_{in}} \right) }=\frac{RT}{F} \ln{ \left( \frac{ [Na^{+}]_{out}}{ [Na^{+}]_{in}} \right) }](images/math/8/4/3/843f1ab5f23a901fd66fe7a27b4a3f27.png)
![E_{X} = 61.5 \log{ \left( \frac{ [X^{+}]_{out}}{ [X^{+}]_{in}} \right) } = -61.5 \log{ \left( \frac{ [X^{-}]_{out}}{ [X^{-}]_{in}} \right) }](images/math/b/f/4/bf4a0a5cc0db1ed0a9e9208fb80017cd.png)
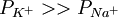 ). If one wanted to calculate the peak voltage of an action potential, one would simply substitute the permeabilities that are present at that time (e.g.
). If one wanted to calculate the peak voltage of an action potential, one would simply substitute the permeabilities that are present at that time (e.g. 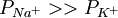 ).
).


