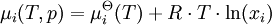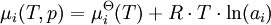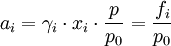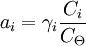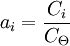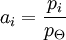Activity (chemistry)

Activity in chemistry is a measure of how different molecules in a non-ideal gas or solution interact with each other.

Activity effects are the result of interactions between ions both electrostatic and covalent. The activity of an ion is influenced by its surroundings. The activity of an ion in a cage of water molecules is different from that in the middle of a counterion cloud.

This type of activity is relevant throughout chemistry from reaction rates to equilibrium constants. For instance large deviations can exist between the calculated hydrogen ion concentration of a strong acid in solution and the hydrogen activity derived from a pH meter or a pH indicator.^[1]

Additional recommended knowledge

Daily Sensitivity Test

Daily Visual Balance Check

Recognize and detect the effects of electrostatic charges on your balance

Definition

In ideal mixtures we can write the dependency of the thermodynamic potential on the composition (written as mole fraction x) as:

We can use this formula to define an activity a, by insisting that the same formulism continues to hold in a non-ideal case.

Obviously a=x in the ideal case.

We can also define an activity coefficient γ:

a_i = γ_ix_i

However there are many alternative schemes to define activity. For dilute solutions usually the solvent follows Raoult's law, but the solute follows Henry's law. It is often convenient to use these laws as a basis for a definition:

Raoult: P_solvent = P*_solvx₂

Henry: P_solute = K_solux₁

Define activities:

a₂ ≡ P_solvent/ P*_solvent

a₁ ≡ P_solute/ K_solute

As K_solute ≠ P*_solute this implies the choice of a different reference point. It represents the extrapolation of the Henry line all the way to x₁ =1 and this is a virtual state: a state of the system that can never be achieved. However, the definition leads to a consistent system of values as long as we do not make x₁ too large.

The same holds if we use molarities or molalities as concentration measures rather than mole fractions. We can safely use such definitions but the meaning of the plimsoll superscript ^o (by lack of better represented as a Θ above) will differ, as we choose a different reference point. This implies that the value of μ^o will be different under these different reference systems.

Molalities are often preferred in this type of calculation because the volumes of non-ideal mixtures are strictly spoken not additive. Molalities do not depend on volume, molarities do.

For a gaseous mixture

The activity is of the form:

where γ_i is the dimensionless fugacity coefficient (fugacity) of the species i, x_i the mole fraction of the species in the gaseous mixture and p the pressure expressed in bar.

The quantity f_i has the dimension of pressure and is fugacity of the gas: for a pure Ideal gas, the fugacity coefficient is equal to one.

The value p₀ is the standard atmospheric pressure. It is equal to 1 bar and is present to cancel the dimensions of the formula.

For compound in a liquid solution

The activity is of the form:

Where γ_i is the coefficient of activity of the species i, C_i is concentration in one of its many measures.

If we (somewhat unwisely) choose to work in molarities the C_o factor is equal to 1 mol·l^-1 and is present to cancel the dimensions of the formula. It also specifies what standard state^o is taken: P=1 bar, T= temperature of interest, concentration = 1 mol/l. When working in molalities this becomes P=1 bar, T= temperature of interest, concentration = 1 mol/kg and in mole fractions P=1 bar, T= temperature of interest, pure compound.

If more than one concentration is to be taken into account, it is in principle possible to do one in molality, the other in mole fraction etc. This does lead to a legitimate choice of standard state and a consistent set of values. (Obviously one might have to convert if comparing with someone else's numbers that are based on a more obvious choice like everything in molality).

In any case, the nature of ^o must be specified. It represents a non-zero standard deliberately chosen to be so (otherwise c/c^o does not exist). It does not represent a natural zero point of any scale. This is also why the superscript ^o is a better reminder than ^o that many different standard states are possible.

Ionic solutions

When the solute undergoes ionic dissociation in solution (a salt e.g.), the system becomes decidedly non-ideal and we need to take the dissociation process into consideration. We can define activities for the cations and anions separately (a₊ and a_-).

It should be noted however that in a liquid solution the activity coefficient of a given ion (e.g. Ca²⁺) isn't measurable because it is experimentally impossible to independently measure the electrochemical potential of an ion in solution. (We cannot add cations without putting in anions at the same time). Therefore one introduces the notions of

mean ionic activity : a_±^ν = a₊^ν+a_-^ν-

mean ionic molality:m_±^ν = m₊^ν+m_-^ν-

mean ionic activity coefficient:γ_±^ν = γ₊^ν+γ_-^ν-

where ν= ν₊+ν_- represent the stoichiometric coefficients involved in the ionic dissociation process

Even though γ₊ and γ_- cannot be determined separately, γ_± is a measureable quantity that can also be predicted for sufficiently dilute systems using Debye-Hückel theory.

For the activity of a strong ionic solute (complete dissociation) we can write:

a₂ = a_±^ν = γ_±^νm_±^ν

Measurement

The most direct way of measuring an activity of a species is to measure its partial vapor pressure in equilibrium with a number of solutions of different strength. For some solutes this is not practical, say sucrose or salt (NaCl) do not have a measurable vapor pressure at ordinary temperatures. However, in such cases it is possible to measure the vapor pressure of the solvent instead. Using the Gibbs-Duhem relation it is possible to translate the change in solvent vapor pressures with concentration into activities for the solute.

Another way to determine the activity of a species is through the manipulation of colligative properties, specifically freezing point depression. Using freezing point depression techniques, it is possible to calculate the activity of a weak acid from the relation,
m^'=m(1+α),
where m^' is the total molal equilibrium concentration of solute determined by any colligative property measurement(in this case ΔT_f, m is the nominal molality obtained from titration and α is the activity of the species.

There are also electrochemical methods that allow the determination of activity and its coefficient.

The value of the mean ionic activity coefficient γ_± of ions in solution can also be estimated with the Debye-Hückel equation, the Davies equation or the Pitzer equation.

Use

Chemical activities should be used to define chemical potentials, where the chemical potential depends on the temperature T, pressure p and the activity a_i according to the formula:

where R is the Ideal Gas Constant and µ_i⁰ is the value of µ_i under standard conditions.

The chemical activities should be used to define the equilibrium constant but in practice often concentrations are used. The same is often true of equtions derived for reaction rates. However, there are circumstances where the activity and the concentration are significantly different and as such, it is not valid to approximate with concentrations where activities are required. Two examples serve this point:

• In a solution of potassium hydrogen iodate at 0.02M the activity is 40% lower than the calculated hydrogen ion concentration resulting in a much higher pH than expected.

• When to a 0.01M hydrochloric acid solution containing Malachite green indicator is added a 5M solution of lithium chloride the color changes from green to yellow indicating increasing acidity when in fact the solution is diluted. Although at low ionic strength (<0.1M) the activation coefficient decreases with increasing ionic strength this coefficient can actually increase with ionic strength in a high ionic strength regime. For hydrochloric acid solutions the minimum is around 0.4M.

Formulae involving activities can be simplified by considering that:

• For a chemical solution:
  • the solvent has an activity of unity
  • At a low concentration, the activity of a solute can be approximated to the ratio of its concentration over the standard concentration:
    
    Therefore, it is approximately equal to its concentration.

• For a mix of gas at low pressure, the activity is equal to the ratio of the partial pressure of the gas over the standard pressure:
  
  Therefore, it is equal to the partial pressure in bars (compared to a standard pressure of 1 bar).

• For a solid body, a uniform, single species solid at one bar has an activity of unity. The same thing holds for a pure liquid.

The latter follows from any definition based on Raoult's law, because if we let the solute concentration x₁ go to zero, the vapor pressure of the solvent P will go to P*. Thus its activity a= P/P* will go to unity. This means that if during a reaction in dilute solution more solvent is generated (the reaction produces water e.g.) we can typically set its activity to unity.

Solid and liquid activities do not depend very strongly on pressure because their molar volumes are typically small. Graphite at 100 bars has an activity of only 1.01 if we choose 1 bar as standard state. Only at very high pressures do we need to worry about such changes.

See also

• Chemical potential
• Concentration
• Debye-Hückel equation
• Fugacity

References

1. ^ pH Paradoxes: Demonstrating That It Is Not True That pH ≡ -log[H+] Christopher G. McCarty and Ed Vitz Journal of Chemical Education Vol. 83 752 2006