To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ideal solutionIn chemistry, an ideal solution or ideal mixture is a solution in which the enthalpy of solution is zero[1]; the closer to zero the enthalpy of solution, the more "ideal" the behavior of the solution becomes. Equivalently, an ideal mixture is one in which the activity coefficients (which measure deviation from ideality) are equal to one.[2] The concept of an ideal solution is fundamental to chemical thermodynamics and its applications, such as the use of colligative properties. Product highlight
Physical originIdeality of solutions is analogous to ideality for gases, with the important difference that intermolecular interactions in liquids are strong and can not simply be neglected as they can for ideal gases. Instead we assume that the mean strength of the interactions are the same between all the molecules of the solution. More formally, for a mix of molecules of A and B, the interactions between unlike neighbors (UAB) and like neighbors UAA and UBB must be of the same average strength i.e. 2UAB=UAA+ UBB and the longer-range interactions must be nil (or at least indistinguishable). If the molecular forces are the same between AA, AB and BB, i.e. UAB=UAA=UBB, then the solution is automatically ideally. If the molecules are almost identical chemically, e.g. 1-butanol and 2-butanol, then the solution will be ideal. Since the interaction energies between A and B are the same, it follows that there is no overall energy (enthalpy) change when the solutions are mixed. The more dissimilar the nature of A and B, the more strongly the solution is expected to deviate from ideality. ConsequencesSince the enthalpy of mixing (solution) is zero, the change in Gibbs free energy on mixing is determined solely by the entropy of mixing. Hence the molar Gibbs free energy of mixing is
or for a two component solution
where m denotes molar i.e. change in Gibbs free energy per mole of solution, and xi is the mole fraction of component i. Note that this free energy of mixing is always negative (since each xi is positive and each lnxi must be negative) i.e. ideal solutions are always completely miscible. The equation above can be expressed in terms of chemical potentials of the individual components
where Δμi,mix = RTlnxi is the change in chemical potential of i on mixing. If the chemical potential of pure liquid i is denoted
where
It can also be shown that volumes are strictly additive for ideal solutions. Non-idealityDeviations from ideality can be described by the use of Margules functions or activity coefficients. A single Margules parameter may be sufficient to describe the properties of the solution if the deviations from ideality are modest; such solutions are termed regular. In contrast to ideal solutions, where volumes are strictly additive and mixing is always complete, the volume of a non-ideal solution is not, in general, the simple sum of the volumes of the component pure liquids and solubility is not guaranteed over the whole composition range. See alsoReferences
Categories: Solutions | Thermodynamics |
|||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ideal_solution". A list of authors is available in Wikipedia. | |||||||||||||||||||||||




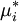 , then the chemical potential of
, then the chemical potential of 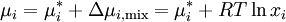
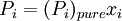
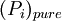 is the equilibrium vapor pressure of the pure component
is the equilibrium vapor pressure of the pure component
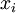 is the
is the 

