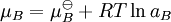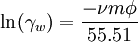To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Activity coefficient
An activity coefficient [1] is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture the interactions between each pair of chemical species are the same (or more formally, the enthalpy of mixing is zero) and, as a result, properties of the mixtures can be be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an activity coefficient. Analogously, expressions involved gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient. Product highlightThese examples can be understood by considering the chemical potential of each substance in the mixture. The chemical potential, μB, of a substance B in an ideal mixture is given by where This is generalised to include non-ideal behaviour by writing when aB is the activity of the substance in the mixture with
where γB is the activity coefficient. As mole fraction or concentration tends of B tends to zero, the behaviour of the mixture more closely approximates to ideal, and so the activity coefficients (of both solute and solvent) tend to unity in very dilute solutions. Note that in general activity coefficients are dimensionless. Modifying mole fractions or concentrations by activity coefficients gives the effective activities of the components, and hence allows expressions such as Raoult's law and equilibrium constants constants to be applied to both ideal and non-ideal mixtures. Knowledge of activity coefficients is particularly important in the context of electrochemistry since the behaviour of electrolyte solutions is often far from ideal, due the effects of the ionic atmosphere. Measurement and prediction of activity coefficientsActivity coefficients may be measured experimentally or calculated theoretically, using the Debye-Hückel equation or extensions such as Davies equation[2] or Pitzer equations[3]. Specific Ion Theory (SIT) [4] may also be used. Alternatively correlative methods such as UNIFAC may be employed, provided fitted model parameters are avaiable For uncharged species, the activity coefficient γ0 mostly follows a "salting-out" model[5]:
This simple model predicts activities of many species (dissolved undissociated gases such as CO2, H2S, NH3, undissociated acids and bases) to high ionic strengths (up to 5 mol/kg). The value of the constant b for CO2 is 0.11 at 10 °C and 0.20 at 330 °C[6][7]. For water, the activity coefficient γw can be calculated using[citation needed]: where ν is the number of ions produced from the dissociation of one molecule of the dissolved salt, m is the molal concentration of the salt dissolved in water, Φ is the osmotic coefficient of water, and the constant 55.51 represents the molal concentration of water. References
Categories: Thermodynamics | Electrochemistry |
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Activity_coefficient". A list of authors is available in Wikipedia. |





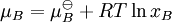
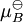 is the chemical potential in the
is the chemical potential in the