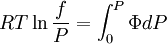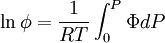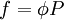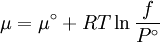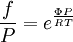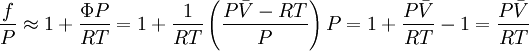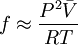To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
FugacityFugacity is a measure of chemical potential in the form of 'adjusted pressure.' It directly relates to the tendency of a substance to prefer one phase (liquid, solid, gas) over another. At a fixed temperature and pressure, water will have a different fugacity for each phase. The phase with the lowest fugacity will be the most favorable; the substance minimizes Gibbs free energy. The concept of fugacity was introduced by American chemist Gilbert N. Lewis in his paper "The osmotic pressure of concentrated solutions, and the laws of the perfect solution." [1] Product highlight
ApplicationsAs well as predicting the preferred phase of a single substance, fugacity is also useful for multi-component equilibrium involving any combination of solid, liquid and gas equilibria. It is useful as an engineering tool for predicting the final phase and reaction state of multi-component mixtures at various temperatures and pressures without doing the actual lab test. Fugacity is not a physical property of a substance; rather it is a calculated property which is intrinsically related to chemical potential. When a system approaches the ideal gaseous state (very low pressure), chemical potential approaches negative infinity, which for the purposes of mathematical modeling is undesirable. Under the same conditions, fugacity approaches zero and the fugacity coefficient (defined below) approaches 1. Thus, fugacity is much easier to manipulate mathematically.
Definition from Statistical MechanicsIn statistical mechanics, the fugacity is one of the parameters that define the grand canonical ensemble (a system that may exchange particles with the environment). It represents the effort of adding an additional particle to the system. Its logarithm, multiplied by where, The grand canonical ensemble is a weighted sum over systems with different numbers of particles. Its partition function, where
while the partition function is related to the pressure Technical detailFugacity is a state function of matter at fixed temperature. It only becomes useful when dealing with substances other than an ideal gas. For an ideal gas, fugacity is equal to pressure. In the real world, though under low pressures and high temperatures some substances approach ideal behavior, no substance is truly ideal, so we use fugacity not only to describe non-ideal gases, but liquids and solids as well. The fugacity coefficient is defined as the ratio fugacity/pressure. For gases at low pressures (where the ideal gas law is a good approximation), fugacity is roughly equal to pressure. Thus, for an ideal gas, the ratio For a given temperature where Thus, for any two mutually-isothermal physical states, represented by subscripts 1 and 2, the ratio of the two fugacities is as follows: Fugacity and chemical potentialFor every pure substance, we have the relation dG = —SdT + VdP for Gibbs free energy and we can integrate this expression remembering the chemical potential is a function of T and P. We must also set a reference state. In this case, for an ideal gas the only reference state will be the pressure, and we set P = 1 bar.
Now, for the ideal gas
Reordering, we get
Which gives the chemical potential for an ideal gas in an isothermal process, where the reference state is P=1 bar. For a real gas, we cannot calculate We would like the expression for a real gas’ chemical potential to be similar to the one for an ideal gas. We can define a magnitude, called fugacity, so that the chemical potential for a real gas becomes
with a given reference state (discussed later). We can see that for an ideal gas, it must be f = P But for
We determine f by defining a function
We can obtain values for Φ experimentally easily by measuring V, T and P. (note that for an ideal gas, Φ = 1) From the expression above we have
We can then write
Where
Since the expression for an ideal gas was chosen to be
Suppose we choose
The fugacity coefficient will then verify
The integral can be evaluated via graphical integration if we measure experimentally values for Φ while varying P. We can then find the fugacity coefficient of a gas at a given pressure P and calculate
The reference state for the expression of a real gas’ chemical potential is taken to be “ideal gas, at P = 1 bar and work T”. Since in the reference state the gas is considered to be ideal (it is an hypothetical reference state), we can write that for the real gas
Alternative methods for calculating fugacityIf we suppose that Φ is constant between 0 and P (assuming it is possible to do this approximation), we have
Expanding in Taylor series about 0,
Finally, we get
This formula allows us to calculate quickly the fugacity of a real gas at P,T, given a value for V (which could be determined using any equation of state), if we suppose is constant between 0 and P. We can also use generalized charts for gases in order to find the fugacity coefficient for a given reduced temperature. Fugacity could be considered a “corrected pressure” for the real gas, but should never be used to replace pressure in equations of state (or any other equations for that matter). That is, it is false to write expressions such as fV = nRT Fugacity is strictly a tool, conveniently defined so that the chemical potential equation for a real gas turns out to be similar to the equation for an ideal gas. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fugacity". A list of authors is available in Wikipedia. |





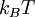 , is the
, is the 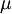
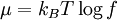
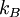 is the
is the 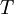 is the temperature. (More commonly, the fugacity is denoted by symbol
is the temperature. (More commonly, the fugacity is denoted by symbol 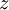 instead of
instead of 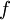 used here. )
In other words, fugacity
used here. )
In other words, fugacity
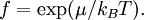
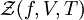 is defined as
is defined as
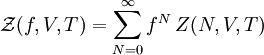
 is the number of particles of the system, and the canonical partition function is defined for a system with a fixed number of particles
is the number of particles of the system, and the canonical partition function is defined for a system with a fixed number of particles  as,
as, 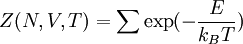 . Here the summation is performed over all microscopic states, and
. Here the summation is performed over all microscopic states, and 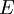 is the energy of each microscopic state. The position of fugacity in grand canonical ensemble is similar to that of temperature in the
is the energy of each microscopic state. The position of fugacity in grand canonical ensemble is similar to that of temperature in the 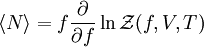 ,
,
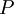 of the system as
of the system as
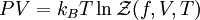 .
.
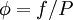 between fugacity
between fugacity 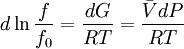
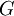 is the
is the 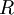 is the
is the 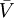 is the fluid's
is the fluid's 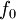 is a reference fugacity which is generally taken as that of an ideal gas at 1 bar. For an ideal gas, when
is a reference fugacity which is generally taken as that of an ideal gas at 1 bar. For an ideal gas, when 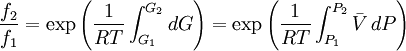
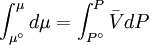
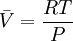
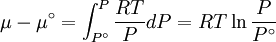
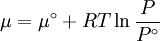
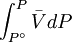 because we do not have a simple expression for a real gas’ molar volume. On the other hand, even if we did have one expression for it (we could use the
because we do not have a simple expression for a real gas’ molar volume. On the other hand, even if we did have one expression for it (we could use the 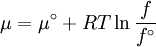
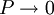 , every gas is an ideal gas. Therefore, fugacity must obey the limit equation
, every gas is an ideal gas. Therefore, fugacity must obey the limit equation
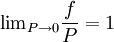
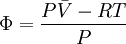
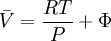
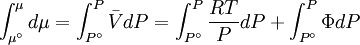
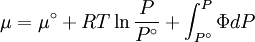
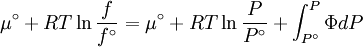
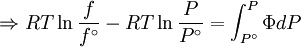
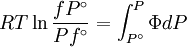
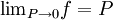 , we obtain
, we obtain