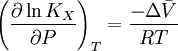To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Equilibrium constant
For a general chemical reaction the equilibrium constant can be defined by[1] where {A} is the activity of the chemical species A etc (activity is a dimensionless quantity). It is conventional to put the activities of the products in the numerator and those of the reactants in the denominator. See Chemical equilibrium for a derivation of this expression. For equilibria in a gas phase, the activity of a gaseous component is the product of the component's partial pressure and the fugacity coefficient for this component. In this case activity is dimensionless as fugacity has the dimension 1/pressure. For equilibria in solution activity is the product of concentration and activity coefficient. It is common practice to determine equilibrium constants in a medium of high ionic strength. In those circumstances the quotient of activity coefficients is effectively constant and the equilibrium constant is taken to be a concentration quotient. However, the value of Kc will depend on the ionic strength. All equilibrium constants depend on temperature and pressure (or volume). A knowledge of equilibrium constants is essential for the understanding of many natural processes such as oxygen transport by haemoglobin in blood and acid-base homeostasis in the human body. Stability constants, formation constants, binding constants, association constants and dissociation constants are all types of equilibrium constant. See also Determination of equilibrium constants for experimental and computational methods. Product highlight
Types of equilibrium constantsCumulative and stepwise formation constantsA cumulative or overall constant, given the symbol β, is the constant for the formation of a complex from reagents. For example, the cumulative constant for the formation of ML2 is given by The stepwise constant, K, for the formation of the same complex from ML and L is given by It follows that A cumulative constant can always be expressed as the product of stepwise constants. There is no agreed notation for stepwise constants, though a symbol such as Competition methodA particular use of a stepwise constant is in the determination of stability constant values outside the normal range for a given method. For example, EDTA complexes of many metals are outside the range for the potentiometric method. The stability constants for those complexes were determined by competition with a weaker ligand. Association and dissociation constantsIn organic chemistry and biochemistry it is customary to use pKa values for acid dissociation equilibria. where Kdiss is a stepwise acid dissociation constant (lg stands for log10). For bases, the base association constant, pKb is used. For any given acid or base the two constants are related by pKa + pKb = pKw, so pKa can always be used in calculations. On the other hand stability constants for metal complexes, and binding constants for host-guest complexes are generally expressed as association constants. When considering equilibria such as it is customary to use association constants for both ML and HL. Also, in generalised computer programs dealing with equilibrium constants it is general practice to use cumulative constants rather than stepwise constants and to omit ionic charges from equilibrium expressions. For example, if NTA, nitrilotriacetic acid, HC(CH2CO2H)3 is designated as H3L and forms complexes ML and MHL with a metal ion M, the following expressions would apply for the dissociation constants. The cumulative association constants can be expressed as Note how the subscripts define the stoichiometry of the equilibrium product. Micro-constantsWhen two or more sites in an asymmetrical molecule may be involved in an equilibrium reaction there are more than one possible equilibrium constants. For example, the molecule L-dopa has two non-equivalent hydroxyl groups which may be deprotonated. Denoting L-Dopa as LH2, the following diagram shows all the species that may be formed (X=CH2CH(NH2)CO2H)
The first protonation constants are
The concentration of LH- is the sum of the concentrations of the two micro-species. Therefore, the equilibrium constant for the reaction, the macro-constant, is the sum of the micro-constants.
In the same way,
Lastly, the cumulative constant is
Thus, although there are six micro-and macro-constants, only three of them are mutually independent. Moreover, the isomerization constant, Ki, is equal to the ratio of the microconstants.
In L-Dopa the isomerization constant is 0.9, so the micro-species L1H and L2H have almost equal concentrations at all pH values. In general a macro-constant is equal to the sum of all the micro-constants and the occupancy of each site is proportional to the micro-constant. The site of protonation can be very important, for example, for biological activity. Micro-constants cannot be determined individually by the usual methods, which give macro-constants. Methods which have been used to determine micro-constants include:
pH considerations (Brønsted constants)pH is defined in terms of the activity of the hydrogen ion If, when determining an equilibrium constant, pH is measured by means of a glass electrode, a mixed equilibrium constant, also known as a Brønsted constant, may result. It all depends on whether the electrode is calibrated by reference to solutions of known activity or known concentration. In the latter case the equilibrium constant would be a concentration quotient. If the electrode is calibrated in terms of known hydrogen ion concentrations it would be better to write p[H] rather than pH, but this suggestion is not generally adopted. Hydrolysis constantsIn aqueous solution the concentration of the hydroxide ion is related to the concentration of the hydrogen ion by The first step in metal ion hydrolysis [4] can be expressed in two different ways It follows that β * = KKW. Hydrolysis constants are usually reported in the β * form and this leads to them appearing to have strange values. For example, if lgK=4 and lg KW=-14, lg β * = 4 -14 = -10. In general when the hydrolysis product contains n hydroxide groups lg β * = lg K + n lg KW Conditional constantsConditional constants, also known as apparent constants, are concentration quotients which are not true equilibrium constants but can be derived from them.[5] A very common instance is where pH is fixed at a particular value. For example, in the case of iron(III) interacting with EDTA, a conditional constant could be defined by This conditional constant will vary with pH. It has a maximum at a certain pH. That is the pH where the ligand sequesters the metal most effectively. In biochemistry equilibrium constants are often measured at a pH fixed by means of a buffer solution. Such constants are, by definition, conditional and different values may be obtained when using different buffers. Temperature dependenceThe van 't Hoff equation. shows that when the reaction is exothermic (ΔH where Cp is the heat capacity at constant pressure The equilibrium constant is related to the standard Gibbs energy change of reaction as where ΔG If the equilibrium constant has been determined and the standard reaction enthalpy has also been determined, by calorimetry, for example, this equation allows the standard entropy change for the reaction to be derived. A more complex formulationThe calculation of KT2 from known KT1 can be approached as follows if standard thermodynamic properties are available. The effect of temperature on equilibrium constant is equivalent to the effect of temperature on Gibbs energy because: where Here, the term "standard" denotes the ideal behaviour (i.e., an infinite dilution) and a hypothetical standard concentration (typically 1 mol/kg). It does not imply any particular temperature or pressure because, although contrary to IUPAC recommendation, it is more convenient when describing aqueous systems over a wide temperature and pressure ranges.[6] The standard Gibbs energy (for each species or for the entire reaction) can be represented (from the basic definitions) as:
In the above equation, the effect of temperature on Gibbs energy (and thus on the equilibrium constant) is ascribed entirely to heat capacity. To evaluate the integrals in this equation, the form of the dependence of heat capacity on temperature needs to be known. Now, if one expresses the standard heat capacity
then the integrals can evaluated and the following final form is obtained: The constants A,B,C,a,b and the absolute entropy, Pressure dependenceThe pressure dependence of the equilibrium constant is usually weak in the range of pressures normally encountered in industry, and therefore, it is usually neglected in practice. This is true for condensed reactant/products (i.e., when reactants and products are solids or liquid) as well as gaseous ones. For a gaseous-reaction example, one may consider the well-studied reaction of hydrogen with nitrogen to produce ammonia: If the pressure is increased by an addition of an inert gas, then neither the composition at equilibrium nor the equilibrium constant are appreciably affected (because the partial pressures remain constant, assuming an ideal-gas behaviour of all gases involved). However, the composition at equilibrium will depend appreciably on pressure when:
In the example reaction above, the number of moles changes from 4 to 2, and an increase of pressure by system compression will result in appreciably more ammonia in the equilibrium mixture. In the general case of a gaseous reaction: the change of mixture composition with pressure can be quantified using: where p denote the partial pressures of the components, P is the total system pressure, X denote the number of moles, Kp is the equilibrium constant expressed in terms of partial pressures and KX is the equilibrium constant expressed in terms of mol fractions. The above change in composition is in accordance with Le Chatelier's principle and does not involve any change of the equilibrium constant with the total system pressure. Indeed, for ideal-gas reactions Kp is independent of pressure. [8]
In a condensed phase, the pressure dependence of the equilibrium constant is associated with the reaction molar volume.[9] For reaction: the reaction molar volume is: where For the above reaction, one can expect the change of the reaction equilibrium constant (based either on mole-fraction or molal-concentration scale) with pressure at constant temperature to be: The matter is complicated as partial molar volume is itself dependent on pressure. Data sourcesIUPAC SC-Database A comprehensive database of published data on equilibrium constants of metal complexes and ligands NIST Standard Reference Database 46 Critically Selected Stability Constants of Metal Complexes Inorganic and organic acids and bases pKa data in water and DMSO See alsoDetermination of equilibrium constants References
Categories: Physical chemistry | Analytical chemistry | Thermodynamics |
||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Equilibrium_constant". A list of authors is available in Wikipedia. |


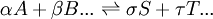
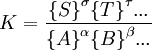
![K_c=\frac{{[S]} ^\sigma {[T]}^\tau ... } {{[A]}^\alpha {[B]}^\beta ...}](images/math/2/b/1/2b116a1f13940176246dd9e08a0c0be3.png)


![M+2L \rightleftharpoons ML_2: [ML_2]=\beta_{12}[M][L]^2](images/math/3/4/b/34b04f239f535297c75c8c1bdc5f834d.png)
![ML+L \rightleftharpoons ML_2: [ML_2]=K[ML][L]=K\beta_{11}[M][[L][L]=K\beta_{11}[M][[L]^2](images/math/1/f/a/1fa0a0fd3924c3b05edb0d193d54d977.png)
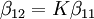
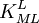 is sometimes found in the literature. It is best always to define each stability constant by reference to an equilibrium expression.
is sometimes found in the literature. It is best always to define each stability constant by reference to an equilibrium expression.
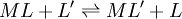
![[ML']=K\frac{[ML][L']}{[L]} = K \frac{\beta_{ML}[M][L][L']}{[L]}= K \beta_{ML}[M][L']: \beta_{ML'}=K\beta_{ML}](images/math/c/e/7/ce7ec46df5b1d8f5981923f463f62ced.png)
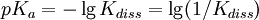
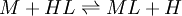
![H_3L \rightleftharpoons H_2L+H:pK_1=-\lg \left(\frac{[H_2L][H]} {[H_3L]} \right)](images/math/6/2/e/62e0f164059185c105bb2bcff9f76ff1.png)
![H_2L \rightleftharpoons HL+H:pK_2=-\lg \left(\frac{[HL][H]} {[H_2L]} \right)](images/math/1/1/3/113efd922e8d6fadb3fed1c056b77c94.png)
![HL \rightleftharpoons L+H:pK_3=-\lg \left(\frac{[L][H]} {[HL]} \right)](images/math/8/2/e/82ea63211b1de248411de3a1dd068541.png)
![L+H \rightleftharpoons HL:\lg \beta_{011} =\lg \left(\frac{[HL]}{[L][H]} \right)=pK_3](images/math/e/d/9/ed9345639885fbc1b79e8a3d47712a44.png)
![L+2H \rightleftharpoons H_2L:\lg \beta_{012} =\lg \left(\frac{[H_2L]}{[L][H]^2} \right)=pK_3+pK_2](images/math/5/7/0/5706e342eaf2dc3b9c831a0cfbc7007e.png)
![L+3H \rightleftharpoons H_3L:\lg \beta_{013} =\lg \left(\frac{[H_3L]}{[L][H]^3} \right)=pK_3+pK_2+pK_1](images/math/1/e/b/1ebdcb5b486bb35f4c960fe34db03ea2.png)
![M+L \rightleftharpoons ML:\lg \beta_{110} =\lg \left(\frac{[ML]}{[M][L]} \right)](images/math/d/4/6/d464edeea84e35a636a75f0803f7f99f.png)
![M+L+H \rightleftharpoons MLH:\lg \beta_{111} =\lg \left(\frac{[MLH]}{[M][L][H]} \right)](images/math/9/2/c/92c4ee766f3b9c3d466d8a5e711a557a.png)
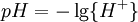
![HL \rightleftharpoons L+H:pK =-\lg \left(\frac{[L]\{H\}}{[HL]} \right)](images/math/e/5/d/e5d922145e1a8def4bdf66cb78305d7c.png)
![K_W=[H][OH]: [OH]=K_W[H]^{-1}\,](images/math/0/6/3/06395af2bb950df6fb44453943fb9d6b.png)
![M(H_2O) \rightleftharpoons M(OH) +H:[M(OH)]=\beta^*[M][H]^{-1}](images/math/7/b/5/7b509a36a1d72e0a432997985836e938.png)
![M+OH \rightleftharpoons M(OH):[M(OH)]=K[M][OH]=K K_W[M][H]^{-1}](images/math/4/f/d/4fdce4f0a46e9cd8572940763f7ea439.png)
![K_{cond}=\frac{[\mbox{Total Fe bound to EDTA}]}{[\mbox{Total Fe not bound to EDTA}]\times [\mbox{Total EDTA not bound to Fe}] }](images/math/f/2/4/f24b6c73e46a03cc6adf856b48c8a081.png)
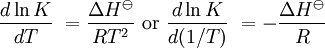
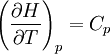
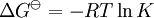
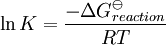
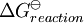 is the reaction standard Gibbs energy, which is the sum of the standard Gibbs energies of the reaction products minus the sum of standard Gibbs energies of reactants.
is the reaction standard Gibbs energy, which is the sum of the standard Gibbs energies of the reaction products minus the sum of standard Gibbs energies of reactants.
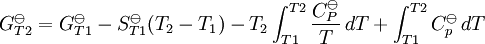
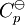 , as a function of absolute temperature using correlations in on of the following forms:
, as a function of absolute temperature using correlations in on of the following forms: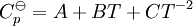
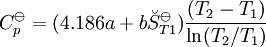
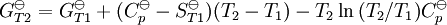
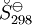 , required for evaluation of
, required for evaluation of 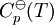 , as well as the values of G298 K and S298 K for many species are tabularized in the literature.
, as well as the values of G298 K and S298 K for many species are tabularized in the literature.
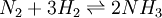
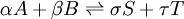
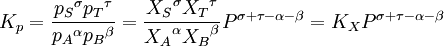
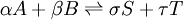
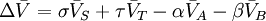
 denotes a partial molar volume of a reactant or a product.
denotes a partial molar volume of a reactant or a product.