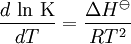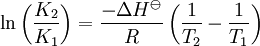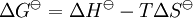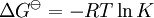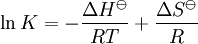My watch list

Van 't Hoff equation

The van 't Hoff equation in chemical thermodynamics relates the change in temperature (T) to the change in the equilibrium constant (K) given the enthalpy change (ΔH). The equation was first derived by Jacobus Henricus van 't Hoff.

$\frac{d \mbox{ ln K}}{dT} = \frac{\Delta H^\ominus}{RT^2}$

Additional recommended knowledge

Recognize and detect the effects of electrostatic charges on your balance

Guide to balance cleaning: 8 simple steps

Weighing the right way

If the enthalpy change of reaction is assumed to be constant with temperature, the definite integral of this differential equation between temperatures T₁ and T₂ is given by

$\ln \left( {\frac{{K_2 }}{{K_1 }}} \right) = \frac{{ - \Delta H^\ominus }}{R}\left( {\frac{1}{{T_2 }} - \frac{1}{{T_1 }}} \right)$

In this equation K₁ is the equilibrium constant at absolute temperature T₁ and K₂ is the equilibrium constant at absolute temperature T₂. ΔH^o is the enthalpy change and R is the gas constant.

Since

$\Delta G^\ominus = \Delta H^\ominus - T\Delta S^\ominus$

and

$\Delta G^\ominus = -RT \ln K$

it follows that

$\ln K = - \frac{{\Delta H^\ominus}}{RT}+ \frac{{\Delta S^\ominus }}{R}$

Therefore, a plot of the natural logarithm of the equilibrium constant versus the reciprocal temperature gives a straight line. The slope of the line is equal to minus the standard enthalpy change divided by the gas constant, ΔH^o/R and the intercept is equal to the standard entropy change divided by the gas constant, ΔS^o/R. Differentiation of this expression yields the van 't Hoff equation.

Category: Thermochemistry