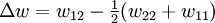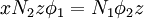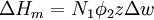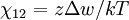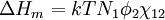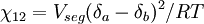To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Flory-Huggins solution theoryFlory-Huggins solution theory is a mathematical model of the thermodynamics of polymer solutions which takes account of the great dissimilarity in molecular sizes in adapting the usual expression for the entropy of mixing. The result is an equation for the Gibbs free energy change ΔGm for mixing a polymer with a solvent. Although it makes simplifying assumptions, it generates useful results for interpreting experiments. The thermodynamic equation for the Gibbs free energy change accompanying mixing at constant temperature and (external) pressure is Product highlightA change, denoted by Δ, is the value of a variable for a solution or mixture minus the values for the pure components considered separately. The objective is to find explicit formulas for ΔHm and ΔSm, the enthalpy and entropy increments associated with the mixing process. The result obtained by Flory and Huggins is The right-hand side is a function of the number of moles n1 and volume fraction φ1 of solvent (component 1), the number of moles n2 and volume fraction φ2 of polymer (component 2), with the introduction of a parameter chi χ to take account of the energy of interdispersing polymer and solvent molecules. R is the gas constant and T is the absolute temperature. The volume fraction is analogous to the mole fraction, but is weighted to take account of the relative sizes of the molecules. For a small solute, the mole fractions would appear instead, and this modification is the innovation due to Flory and Huggins. DerivationWe first calculate the entropy of mixing, the increase in the uncertainty about the locations of the molecules when they are interspersed. In the pure condensed phases — solvent and polymer — everywhere we look we find a molecule. Of course, any notion of "finding" a molecule in a given location is a thought experiment since we can't actually examine spatial locations the size of molecules. The expression for the entropy of mixing of small molecules in terms of mole fractions is no longer reasonable when the solute is a macromolecular chain. We take account of this dissymmetry in molecular sizes by assuming that individual polymer segments and individual solvent molecules occupy sites on a lattice. Each site is occupied by exactly one molecule of the solvent or by one monomer of the polymer chain, so the total number of sites is N1 is the number of solvent molecules and N2 is the number of polymer molecules, each of which has x segments. From statistical mechanics we can calculate the entropy change, the increase in spatial uncertainty, as a result of mixing solute and solvent. where k is Boltzmann's constant. Define the lattice volume fractions φ1 and φ2 These are also the probabilities that a given lattice site, chosen at random, is occupied by a solvent molecule or a polymer segment, respectively. Thus For a small solute whose molecules occupy just one lattice site, x equals one, the volume fractions reduce to molecular or mole fractions, and we recover the usual equation from ideal mixing theory. In addition to the entropic effect, we can expect an enthalpy change. There are three molecular interactions to consider: solvent-solvent w11, monomer-monomer w22 (not the covalent bonding, but between different chain sections), and monomer-solvent w12. Each of the last occurs at the expense of the average of the other two, so the energy increment per monomer-solvent contact is The total number of such contacts is where z is the coordination number, the number of nearest neighbors for a lattice site, each one occupied either by one chain segment or a solvent molecule. That is, xN2 is the total number of polymer segments (monomers) in the solution, so xN2z is the number of nearest-neighbor sites to all the polymer segments. Multiplying by the probability φ1 that any such site is occupied by a solvent molecule, we obtain the total number of polymer-solvent molecular interactions. The enthalpy change is equal to the energy change per polymer monomer-solvent interaction multiplied by the number of such interactions The polymer-solvent interaction parameter chi is defined as It depends on the nature of both the solvent and the solute, and is the only material-specific parameter in the model. The enthalpy change becomes Assembling terms, the total free energy change is where we have converted the expression from molecules N1 and N2 to moles n1 and n2 by transferring Avogadro's number NA to the gas constant R = kNA. The value of the interaction parameter can be estimated from the Hildebrand solubility parameters δa and δb where Vseg is the actual volume of a polymer segment. This treatment does not attempt to calculate the conformational entropy of folding for polymer chains. (See the random coil discussion.) The conformations of even amorphous polymers will change when they go into solution, and most thermoplastic polymers also have lamellar crystalline regions which do not persist in solution as the chains separate. These events are accompanied by additional entropy and energy changes. More advanced models exist, such as the Flory-Krigbaum theory. References and footnotes
Categories: Polymer chemistry | Solutions | Free energy | Thermodynamics | Statistical mechanics |
||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Flory-Huggins_solution_theory". A list of authors is available in Wikipedia. | ||||||||||


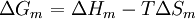



![\Delta G_m = RT[\,n_1\ln\phi_1 + n_2\ln\phi_2 + n_1\phi_2\chi_{12}\,] \,](images/math/a/e/a/aea39e7f9ec0ac97923925da507d0a8f.png)
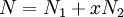
![\Delta S_m = -k[\,N_1\ln(N_1/N) + N_2\ln(xN_2/N)\,]\,](images/math/6/8/d/68d81c2c2e582c5748ebe4d38f8585d8.png)
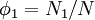
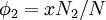
![\Delta S_m = -k[\,N_1\ln\phi_1 + N_2\ln\phi_2\,]\,](images/math/a/d/4/ad483068b31a8642d6a264ea29b3e725.png)