To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Liouville's theorem (Hamiltonian)
There are also related mathematical results in symplectic topology and ergodic theory. Product highlight
Liouville equationThe Liouville equation describes the time evolution of phase space distribution function (while measure is the correct term from mathematics, physicists generally call it a distribution). Consider a dynamical system with canonical coordinates qi and conjugate momenta pi, where Time derivatives are denoted by dots, and are evaluated according to Hamilton's equations for the system. This equation demonstrates the conservation of density in phase space (which was Gibbs's name for the theorem). Liouville's theorem states that
A simple proof of the theorem is to observe that the evolution of ρ is defined by the continuity equation: That is, the tuplet where H is the Hamiltonian, and Hamilton's equations have been used. That is, viewing the motion through phase space as a 'fluid flow' of system points, the theorem that the convective derivative of the density dρ / dt is zero follows from the equation of continuity by noting that the 'velocity field' Another illustration is to consider the trajectory of a cloud of points through phase space. It is straightforward to show that as the cloud stretches in one coordinate – pi say – it shrinks in the corresponding qi direction so that the product ΔpiΔqi remains constant. Equivalently, the existence of a conserved current implies, via Noether's theorem, the existence of a symmetry. The symmetry is invariance under time translations, and the generator (or Noether charge) of the symmetry is the Hamiltonian. Physical interpretationThe expected total number of particles is the integral over phase space of the distribution: A normalizing factor is conventionally included in the phase space measure but has here been omitted. In the simple case of a nonrelativistic particle moving in Euclidean space under a force field This is different from the Vlasov equation, or sometimes the Collisionless Boltzmann Equation, in astrophysics. The latter, which has a 6-D phase space, is used to describe the evolution of a large number of collisionless particles moving under the influence of gravity and/or electromagnetic field. In classical statistical mechanics, the number of particles N is very large, (typically of order Avogadro's number, for a laboratory-scale system). Setting See also canonical ensemble and microcanonical ensemble Other formulationsPoisson bracketThe theorem is often restated in terms of the Poisson bracket as or in terms of the Liouville operator or Liouvillian, as Ergodic theoryIn ergodic theory and dynamical systems, motivated by the physical considerations given so far, there is a corresponding result also referred to as Liouville's theorem. In Hamiltonian mechanics, the phase space is a smooth manifold that comes naturally equipped with a smooth measure (locally, this measure is the 6n-dimensional Lebesgue measure). The theorem says this smooth measure is invariant under the Hamiltonian flow. More generally, one can describe the necessary and sufficient condition under which a smooth measure is invariant under a flow. The Hamiltonian case then becomes a corollary. Symplectic geometryIn terms of symplectic geometry, the theorem states that the d-power of the symplectic structure (2-form, formed by summation of the wedge products of Δpi and Δqi) has a zero Lie derivative for its Hamiltonian evolution. (The d-power of the symplectic structure is just the measure on the phase space described above.) In fact, the symplectic structure itself is preserved (not only the d-power). For this reason, in this context, symplectic structure is also called Poincaré invariant. Hence the theorem about Poincaré invariant is a generalization of the Liouville's theorem. Further generalization is also possible. In the frame of invariant Hamiltonian formalism, the theorem about existence of symplectic structure on invariant phase space turns out to be a deep generalization of the theorem about Poincaré invariant. Quantum mechanicsThe analog of Liouville equation in quantum mechanics describes the time evolution of a mixed state. Canonical quantization yields a quantum-mechanical version of this theorem. This procedure, often used to devise quantum analogues of classical systems, involves describing a classical system using Hamiltonian mechanics. Classical variables are then re-interpreted as quantum operators, while Poisson brackets are replaced by commutators. In this case, the resulting equation is where ρ is the density matrix. When applied to the expectation value of an observable, the corresponding equation is given by Ehrenfest's theorem, and takes the form where A is an observable. Note the sign difference, which follows from the assumption that the operator is stationary and the state is time-dependent. Remarks
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Liouville's_theorem_(Hamiltonian)". A list of authors is available in Wikipedia. |





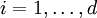 . Then the phase space distribution
. Then the phase space distribution 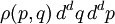 that a particle will be found in the infinitesimal phase space volume
that a particle will be found in the infinitesimal phase space volume 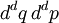 . The Liouville equation governs the evolution of
. The Liouville equation governs the evolution of 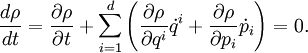
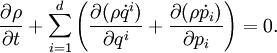
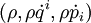 is a conserved current. Notice that the difference between this and Liouville's equation are the terms
is a conserved current. Notice that the difference between this and Liouville's equation are the terms
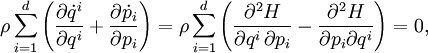
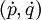 in phase space has zero divergence (which follows from Hamilton's relations).
in phase space has zero divergence (which follows from Hamilton's relations).
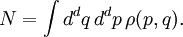
 with coordinates
with coordinates 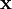 and momenta
and momenta 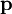 , Liouville's theorem can be written
, Liouville's theorem can be written
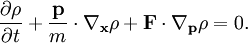
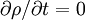 gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given
gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given 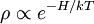 , where
, where 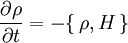
![\hat{\mathbf{L}}=\sum_{i=1}^{d}\left[\frac{\partial H}{\partial p_{i}}\frac{\partial}{\partial q^{i}}-\frac{\partial H}{\partial q^{i}}\frac{\partial }{\partial p_{i}}\right],](images/math/5/4/a/54a6e9dc8b797209699b78b6238657bb.png)
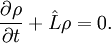
![\frac{\partial}{\partial t}\rho=-\frac{i}{\hbar}[H,\rho]](images/math/2/0/6/2068fad29535cd763e5e6b774d9614e4.png)
![\frac{d}{dt}\langle A\rangle = \frac{i}{\hbar}\langle [H,A] \rangle](images/math/c/9/3/c9308d63e2e53236ad2fcc9d513548b5.png)


