To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Convective derivativeThe convective derivative (also commonly known as the advective derivative, substantive derivative, or the material derivative) is a derivative taken with respect to a coordinate system moving with velocity u, and is often used in fluid mechanics and classical mechanics. Product highlightφ is a scalar valued function of stationary spatial coordinates. v is a vector valued function of stationary spatial coordinates. The convective derivative is defined as: where The convective derivative expresses the Eulerian derivative (written Consider water undergoing steady flow through a hosepipe that has a gradually decreasing cross section. Because water is incompressible in practice, conservation of mass requires that the flow is faster at the end of the pipe than at the start. Because the flow is steady, the Eulerian derivative of velocity is everywhere zero, but the convective derivative is nonzero because any individual parcel of fluid accelerates as it moves down the hose. For tensor fields we usually want to take into account not only translation of the coordinate system due to the fluid movement but also its rotation and stretching. This is achieved by the upper convected time derivative. There are many other names for this operator, including the Lagrangian derivative, total time derivative, Stokes derivative, particle derivative, and material derivative.
ProofProof is via the multivariate chain rule. In tensor notation (with the Einstein summation convention), the derivation may be written: See alsoReferences
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Convective_derivative". A list of authors is available in Wikipedia. |





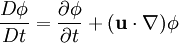
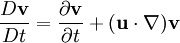
 is the gradient operator del and
is the gradient operator del and 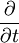 denotes the partial derivative with respect to t. The name is derived from the
denotes the partial derivative with respect to t. The name is derived from the 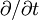 ) in
) in ![\left[\frac{D\mathbf{B}}{Dt}\right]_j = \frac{D}{D t}(\hat{B_j}(t, x_i(t))) = \frac{\partial B_j}{\partial t} + \frac{\partial B_j}{\partial x_i} \frac{\partial x_i}{\partial t} = \frac{\partial B_j}{\partial t} + \frac{\partial x_i}{\partial t} \frac{\partial}{\partial x_i} B_j = \frac{\partial B_j}{\partial t} + \left[(\mathbf{u}\cdot\nabla)\mathbf{B}\right]_j](images/math/a/0/9/a098cfe33e2849a1b6842443c51a088e.png)


