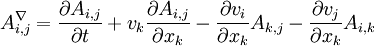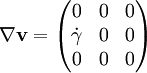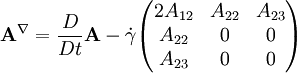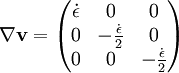To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Upper convected time derivativeIn continuum mechanics, including fluid dynamics upper convected time derivative or Oldroyd derivative is the rate of change of some tensor property of a small parcel of fluid that is written in the coordinate system rotating and stretching with the fluid. The operator is specified by the following formula: where:
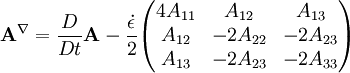
The formula can be rewritten as: By definition the upper convected time derivative of the Finger tensor is always zero. The upper convected derivatives is widely use in polymer rheology for the description of behavior of a visco-elastic fluid under large deformations. Product highlight
Examples for the symmetric tensor ASimple shearFor the case of simple shear: Thus, Uniaxial extension of uncompressible fluidIn this case a material is stretched in the direction X and compresses in the direction s Y and Z, so to keep volume constant. The gradients of velocity are: Thus, See alsoReferences
Categories: Fluid dynamics | Non-Newtonian fluids |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Upper_convected_time_derivative". A list of authors is available in Wikipedia. |


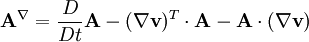
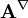 is the Upper convected time derivative of a tensor field
is the Upper convected time derivative of a tensor field 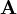
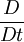 is the
is the 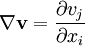 is the tensor of velocity derivatives for the fluid.
is the tensor of velocity derivatives for the fluid.