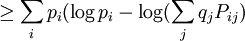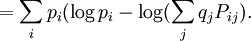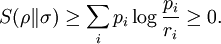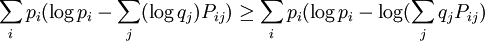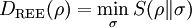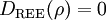To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Quantum relative entropyIn quantum information theory, quantum relative entropy is a measure of distinguishability between two quantum states. It is the quantum mechanical analog of relative entropy. Product highlight
MotivationFor simplicity, it will be assumed that all objects in the article are finite dimensional. We first discuss the classical case. Suppose the probabilities of a finite sequence of events is given by the probability distribution P = {p1...pn}, but somehow we mistakenly assumed it to be Q = {q1...qn}. For instance, we can mistake an unfair coin for a fair one. According to this erroneous assumption, our uncertainty about the j-th event, or equivalently, the amount of information provided after observing the j-th event, is The (assumed) average uncertainty of all possible events is then On the other hand, the Shannon entropy of the probability distribution p, defined by is the real amount of uncertainty before observation. Therefore the difference between these two quantities is a measure of the distinguishability of the two probability distributions p and q. This is precisely the classical relative entropy, or Kullback–Leibler divergence: Note
DefinitionAs with many other objects in quantum information theory, quantum relative entropy is defined by extending the classical definition from probability distributions to density matrices. Let ρ be a density matrix. The von Neumann entropy of ρ, which is the quantum mechanical analaog of the Shannon entropy, is given by For two density matrices ρ and σ, the quantum relative entropy of ρ with respect to σ is defined by We see that, when the states are classical, i.e. ρσ = σρ, the definition coincides with the classical case. Non-finite relative entropyIn general, the support of a matrix M, denoted by supp(M), is the orthogonal complement of its kernel. When consider the quantum relative entropy, we assume the convention that - s· log 0 = ∞ for any s > 0. This leads to the definition that when This makes physical sense. Informally, the quantum relative entropy is a measure of our ability to distinguish two quantum states. But orthogonal quantum states can always be distinguished, via projective measurement. In the present context, this is reflected by non-finite quantum relative entropy. In the interpretation given in the previous section, if we erroneously assume the state ρ has support in supp(ρ)⊥, this is an error impossible to recover from. Klein's inequalityCorresponding classical statementFor the classical Kullback–Leibler divergence, it can be shown that and equality holds if and only if P = Q. Colloquially, this means that the uncertainty calculated using erroneous assumptions is always greater than the real amount of uncertainty. To show the inequality, we rewrite Notice that log is a concave function. Therefore -log is convex. Applying Jensen's inequality to -log gives Jensen's inequality also states that equality holds if and only if, for all i, qi = (∑qj) pi, i.e. p = q. The resultKlein's inequality states that the quantum relative entropy is non-negative in general. It is zero if and only ρ = σ. Proof Let ρ and σ have spectral decompositions So Direct calculation gives
Since the matrix (Pi j)i j is a doubly stochastic matrix and -log is a concave function, the above expression is Define ri = ∑jqj Pi j. Then {ri} is a probability distribution. From the non-negativity of classical relative entropy, we have The second part of the claim follows from the fact that, since -log is strictly convex, equality is achieved in if and only if (Pi j) is a permutation matrix, which implies ρ = σ, after a suitable labeling of the eigenvectors {vi} and {wi}. An entanglement measureLet a composite quantum system have state space and ρ be a density matrix acting on H. The relative entropy of entanglement of ρ is defined by where the minimum is taken over the family of separable states. A physical interpretation of the quantity is the optimal distinguishability of the state ρ from separable states. Clearly, when ρ is not entangled by Klein's inequality. |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Quantum_relative_entropy". A list of authors is available in Wikipedia. |





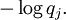
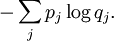
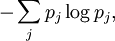
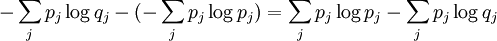
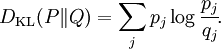
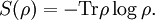
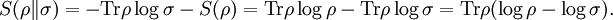
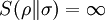
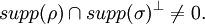
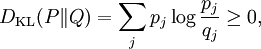
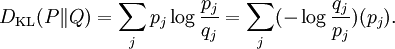
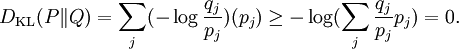
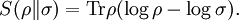
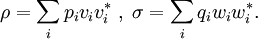
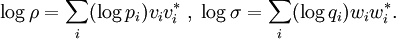
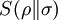
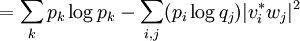
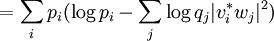
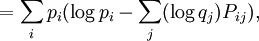 where Pi j = |vi*wj|2.
where Pi j = |vi*wj|2.