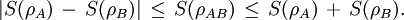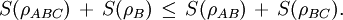To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Von Neumann entropyIn quantum statistical mechanics, von Neumann entropy refers to the extension of classical entropy concepts to the field of quantum mechanics. Product highlightJohn von Neumann rigorously established the correct mathematical framework for quantum mechanics with his work Mathematische Grundlagen der Quantenmechanik. He provided in this work a theory of measurement, where the usual notion of wave collapse is described as an irreversible process (the so called von Neumann or projective measurement). IntroductionThe density matrix was introduced, with different motivations, by von Neumann and by Lev Landau. The motivation that inspired Landau was the impossibility of describing a subsystem of a composite quantum system by a state vector. On the other hand, von Neumann introduced the density matrix in order to develop both quantum statistical mechanics and a theory of quantum measurements. The density matrix formalism was developed to extend the tools of classical statistical mechanics to the quantum domain. In the classical framework we compute the partition function of the system in order to evaluate all possible thermodynamic quantities. Von Neumann introduced the density matrix in the context of states and operators in a Hilbert space. The knowledge of the statistical density matrix operator would allow us to compute all average quantities in a conceptually similar, but mathematically different way. Let us suppose we have a set of wave functions After this procedure, one finally arrives at the density matrix formalism when seeking a form where p(n1,n2,...,nN) is invariant with respect to the representation used. In the form it is written, it will only yield the correct expectation values for quantities which are diagonal with respect to the quantum numbers n1,n2,...,nN. Expectation values of operators which are not diagonal involve the phases of the quantum amplitudes. Suppose we encode the quantum numbers n1,n2,...,nN into the single index i or j. Then our wave function has the form The expectation value of an operator B which is not diagonal in these wave functions, so The role which was originally reserved for the quantities | ai | 2 is thus taken over by the density matrix of your system S. Therefore EB reads as The invariance of the above term is described by matrix theory. We described a mathematical framework where the expectation value of quantum operators, as described by matrices, is obtained by taking the trace of the product of the density operator Given the density matrix ρ , von Neumann defined the entropy as which is a proper extension of the Gibbs entropy (and the Shannon entropy) to the quantum case. To compute (\ref{Sv}) one has to find a basis in which ρ possesses a diagonal representation. We note that the entropy S(ρ) times the Boltzmann constant kB equals the thermodynamical or physical entropy. If the system is finite (finite dimensional matrix representation) the entropy (\ref{Sv}) describes the departure of our system from a pure state. In other words, it measures the degree of mixture of our state describing a given finite system. Properties of the von Neumann entropy
Instead, if ρA,ρB are the reduced density matrices of the general state ρAB, then This property is known as subadditivity. While in Shannon's theory the entropy of a composite system can never be lower than the entropy of any of its parts, in quantum theory this is not the case. Actually, this can be seen as an indicator of an entangled state ρAB.
The von Neumann entropy is being extensively used in different forms (conditional entropies, relative entropies, etc.) in the framework of quantum information theory. Entanglement measures are based upon some quantity directly related to the von Neumann entropy. However, there have appeared in the literature several papers dealing with the possible inadequacy of the Shannon information measure, and consequently of the von Neumann entropy as an appropriate quantum generalization of Shannon entropy. The main argument is that in classical measurement the Shannon information measure is a natural measure of our ignorance about the properties of a system, whose existence is independent of measurement. Conversely, quantum measurement cannot be claimed to reveal the properties of a system that existed before the measurement was made. This controversy has encouraged some authors to introduce the non-additivity property of Tsallis' entropy (a generalization of the standard Boltzmann-Gibbs entropy) as the main reason for recovering a true quantal information measure in the quantum context, claiming that non-local correlations ought to be described because of the particularity of Tsallis' entropy. In 2004 A. Stotland, A.A. Pomeransky, E. Bachmat and D. Cohen have introduced a new definition of entropy that reflects the inherent uncertainty of quantum mechanical states. This proper definition allows to distinguish between the minimum uncertainty entropy of pure states, and the excess statistical entropy of mixtures. Furthermore this proper definition satisfies the basic inequalities of information theory. References
Categories: Statistical mechanics | Thermodynamic entropy | Quantum mechanical entropy |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Von_Neumann_entropy". A list of authors is available in Wikipedia. |
- Future-oriented expansion of the LUM management
- Learn How to Comply with the ISO 8655 Revisions for Pipettes - A Guide to the Routine Testing and Calibration of Pipettes
- EB-Soft Gesellschaft fuer elektronische Beschriftungs-Software mbH - Heilbronn, Germany
- Hunter Associates Laboratory, Inc. - Reston, Stati Uniti d'America





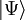 which depend parametrically on a set of quantum numbers
which depend parametrically on a set of quantum numbers 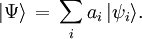
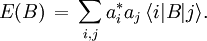
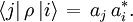
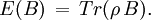
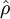 and an operator
and an operator 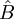 (Hilbert scalar product between operators). The matrix formalism here is in the statistical mechanics framework, although it applies as well for finite quantum systems, which is usually the case, where the state of the system cannot be described by a pure state, but as a statistical operator
(Hilbert scalar product between operators). The matrix formalism here is in the statistical mechanics framework, although it applies as well for finite quantum systems, which is usually the case, where the state of the system cannot be described by a pure state, but as a statistical operator 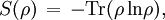
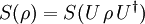 , with
, with 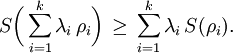
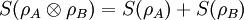 .
.