To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Perplexity
Product highlight
Perplexity of a probability distributionThe perplexity of a discrete probability distribution p is defined as where H(p) is the entropy of the distribution and x ranges over events. One may also define the perplexity of a random variable X as the perplexity of the distribution over its possible values x. It is easy to see that in the special case where p models a fair k-sided die (a uniform distribution over k discrete events), its perplexity is k. We may therefore regard any random variable with perplexity k as having the same uncertainty as a fair k-sided die. We are "k-ways perplexed" about the value of such a random variable. (Unless it is also a fair k-sided die, more than k values will be possible, but the overall uncertainty is no greater because some of these values will have probability greater than 1/k.) Perplexity of a probability modelOften one tries to model an unknown probability distribution p, based on a training sample that was drawn from p. Given a proposed probability model q, one may evaluate q by asking how well it predicts a separate test sample x1, x2, ..., xN also drawn from p. The perplexity of the model q is defined as Better models q of the unknown distribution p will tend to assign higher probabilities q(xi) to the test events. Thus, they have lower perplexity: they are less surprised by the test sample. The exponent above may be regarded as the average number of bits needed to represent a test event xi if one uses an optimal code based on q. Low-perplexity models do a better job of compressing the test sample, requiring few bits per test element on average because q(xi) tends to be high. The exponent may also be regarded as a cross-entropy, where Perplexity per wordIn natural language processing, perplexity is a common way of evaluating language models. A language model is a probability distribution over entire sentences or texts. Using the definition above, one might find that the average sentence xi in the test sample could be coded in 190 bits (i.e., the test sentences had an average log-probability of -190). This would give an enormous model perplexity of 2190 per sentence. However, it is more common to normalize for sentence length and consider only the number of bits per word. Thus, if the test sample's sentences comprised a total of 1,000 words, and could be coded using a total of 7,950 bits, one could report a model perplexity of 27.95 = 247 per word. In other words, the model is as confused on test data as if it had to choose uniformly and independently among 247 possibilities for each word. The lowest perplexity that has been published on the Brown Corpus (1 million words of American English of varying topics and genres) is indeed about 247 per word, corresponding to a cross-entropy of log2247 = 7.95 bits per word or 1.75 bits per letter [1]. It is often possible to achieve lower perplexity on more specialized corpora, as they are more predictable. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Perplexity". A list of authors is available in Wikipedia. |





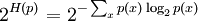
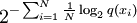
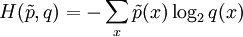
 denotes the empirical distribution of the test sample (i.e.,
denotes the empirical distribution of the test sample (i.e., 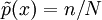 if x appeared n times in the test sample of size N).
if x appeared n times in the test sample of size N).


