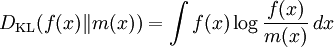To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Entropy in thermodynamics and information theory
There are close parallels between the mathematical expressions for the thermodynamic entropy, usually denoted by S, of a physical system in the statistical thermodynamics established by Ludwig Boltzmann and J. Willard Gibbs in the 1870s; and the information-theoretic entropy, usually expressed as H, of Claude Shannon and Ralph Hartley developed in the 1940s. Shannon, although not initially aware of this similarity, commented in it upon publicizing information theory in A Mathematical Theory of Communication. This article explores what links there are between the two concepts, and how far they can be regarded as connected. Product highlightEquivalence of form of the defining expressionsDiscrete caseThe defining expression for entropy in the theory of statistical mechanics established by Ludwig Boltzmann and J. Willard Gibbs in the 1870s, is of the form: where pi is the probability of the microstate i taken from an equilibrium ensemble. The defining expression for entropy in the theory of information established by Claude E. Shannon in 1948 is of the form: where pi is the probability of the message mi taken from the message space M. Mathematically H may also be seen as an average information, taken over the message space, because when a certain message occurs with probability pi, the information -log(pi) will be obtained. If all the microstates are equiprobable (a microcanonical ensemble), the statistical thermodynamic entropy reduces to the form on Boltzmann's tombstone, where W is the number of microstates. If all the messages are equiprobable, the information entropy reduces to the Hartley entropy where | M | is the cardinality of the message space M. The logarithm in the thermodynamic definition is the natural logarithm. It can be shown that the Gibbs entropy formula, with the natural logarithm, reproduces all of the properties of the macroscopic classical thermodynamics of Clausius. (See article: Entropy (statistical views)). The logarithm can also be taken to the natural base in the case of information entropy. This is equivalent to choosing to measure information in nats instead of the usual bits. In practice, information entropy is almost always calculated using base 2 logarithms, but this distinction amounts to nothing other than a change in units. One nat is about 1.44 bits. The presence of Boltzmann's constant k in the thermodynamic definitions is a historical accident, reflecting the conventional units of temperature. It is there to make sure that the statistical definition of thermodynamic entropy matches the classical entropy of Clausius, thermodynamically conjugate to temperature. For a simple compressible system that can only perform volume work, the first law of thermodynamics becomes But one can equally well write this equation in terms of what physicists and chemists sometimes call the 'reduced' or dimensionless entropy, σ = S/k, so that Just as S is conjugate to T, so σ is conjugate to kT (the energy that is characteristic of T on a molecular scale). Continuous caseThe most obvious extension of the Shannon entropy is the differential entropy, As long as f(x) is a probability density function, p. d. f., H repesents the average information (entropy, disorder, diversity etcetera) of f(x). For any uniform p. d. f. f(x), the exponential of H is the volume covered by f(x) (in analogy to the cardinality in the discrete case). The volume covered by a n-dimensional multivariate Gaussian distribution with moment matrix M is proportional to the volume of the ellipsoid of concentration and is equal to square root{ (2 pi e)n determinant(M) }. The volume is always positive. Average information may be maximized using Gaussian adaptation - one of the evolutionary algorithms - keeping the mean fitness - i. e. the probability of becoming a parent to new individuals in the population - constant (and without the need for any knowledge about average information as a criterion function). This is illustrated by the figure below, showing Gaussian adaptation climbing a mountain crest in a phenotypic landscape. The lines in the figure are part of a contour line enclosing a region of acceptability in the landscape. At the start the cluster of red points represents a very homogeneous population with small variances in the phenotypes. Evidently, even small environmental changes in the landscape, may cause the process to become extinct.
After a sufficiently large number of generations, the increase in average information may result in the green cluster. Actually, the mean fitness is the same for both red and green cluster (about 65%). The effect of this adaptation is not very salient in a 2-dimensional case, but in a high-dimensional case, the efficiency of the search process may be increased by many orders of magnitude. Besides, a Gaussian distribution has the highest average information as compared to other distributions having the same second order moment matrix (Middleton 1960). But it turns out that this is not in general a good measure of uncertainty or information. For example, the differential entropy can be negative; also it is not invariant under continuous co-ordinate transformations. More useful for the continuous case is the relative entropy of a distribution, defined as the Kullback-Leibler divergence from the distribution to a reference measure m(x), (or sometimes the negative of this). The relative entropy carries over directly from discrete to continuous distributions, and is invariant under co-ordinate reparamatrisations. For an application of relative entropy in a quantum information theory setting, see eg [1]. Theoretical relationshipDespite all that, there is an important difference between the two quantities. The information entropy H can be calculated for any probability distribution (if the "message" is taken to be that the event i which had probability pi occurred, out of the space of the events possible). But the thermodynamic entropy S refers to thermodynamic probabilities pi specifically. Furthermore, the thermodynamic entropy S is dominated by different arrangements of the system, and in particular its energy, that are possible on a molecular scale. In comparison, information entropy of any macroscopic event is so small as to be completely irrelevant. However, a connection can be made between the two, if the probabilities in question are the thermodynamic probabilities pi: the (reduced) Gibbs entropy σ can then be seen as simply the amount of Shannon information needed to define the detailed microscopic state of the system, given its macroscopic description. Or, in the words of G. N. Lewis writing about chemical entropy in 1930, "Gain in entropy always means loss of information, and nothing more". To be more concrete, in the discrete case using base two logarithms, the reduced Gibbs entropy is equal to the minimum number of yes/no questions that need to be answered in order to fully specify the microstate, given that we know the macrostate. Furthermore, the prescription to find the equilibrium distributions of statistical mechanics, such as the Boltzmann distribution, by maximising the Gibbs entropy subject to appropriate constraints (the Gibbs algorithm), can now be seen as something not unique to thermodynamics, but as a principle of general relevance in all sorts of statistical inference, if it desired to find a maximally uninformative probability distribution, subject to certain constraints on the behaviour of its averages. (These perspectives are explored further in the article Maximum entropy thermodynamics). Information is physical: (1) Szilard's engineA neat physical thought-experiment demonstrating how just the possession of information might in principle have thermodynamic consequences was established in 1929 by Szilard, in a refinement of the famous Maxwell's demon scenario. Consider Maxwell's set-up, but with only a single gas particle in a box. If the supernatural demon knows which half of the box the particle is in (equivalent to a single bit of information), it can close a shutter between the two halves of the box, close a piston unopposed into the empty half of the box, and then extract kBTln2 joules of useful work if the shutter is opened again. The particle can then be left to isothermally expand back to its original equilibrium occupied volume. In just the right circumstances therefore, the possession of a single bit of Shannon information (a single bit of negentropy in Brillouin's term) really does correspond to a reduction in physical entropy, which theoretically can indeed be parlayed into useful physical work. Information is physical: (2) Landauer's principleIn fact one can generalise: any information that has a physical representation must somehow be embedded in the statistical mechanical degrees of freedom of a physical system. Thus, Rolf Landauer argued in 1961, if one were to imagine starting with those degrees of freedom in a thermalised state, there would be a real reduction in thermodynamic entropy if they were then re-set to a known state. This can only be achieved under information-preserving microscopically deterministic dynamics if the uncertainty is somehow dumped somewhere else — ie if the entropy of the environment (or the non information-bearing degrees of freedom) is increased by at least an equivalent amount, as required by the Second Law, by gaining an appropriate quantity of heat: specifically kT ln 2 of heat for every 1 bit of randomness erased. On the other hand, Landauer argued, there is no thermodynamic objection to a logically reversible operation potentially being achieved in a physically reversible way in the system. It is only logically irreversible operations — for example, the erasing of a bit to a known state, or the merging of two computation paths — which must be accompanied by a corresponding entropy increase. Applied to the Maxwell's demon/Szilard engine scenario, this suggests that it might be possible to "read" the state of the particle into a computing apparatus with no entropy cost; but only if the apparatus has already been SET into a known state, rather than being in a thermalised state of uncertainty. To SET (or RESET) the apparatus into this state will cost all the entropy that can be saved by knowing the state of Szilard's particle. NegentropyShannon entropy has been related by physicist Léon Brillouin to a concept sometimes called negentropy. In his 1962 book Science and Information Theory, Brillouin described the Negentropy Principle of Information or NPI, the gist of which is that acquiring information about a system’s microstates is associated with a decrease in entropy (work is needed to extract information, erasure leads to increase in thermodynamic entropy).[1] There is no violation of the second law of thermodynamics, according to Brillouin, since a reduction in any local system’s thermodynamic entropy results in an increase in thermodynamic entropy elsewhere. Negentropy is a controversial concept as it yields Carnot efficiency higher than one. Black holesStephen Hawking often speaks of the thermodynamic entropy of black holes in terms of their information content. Do black holes destroy information? See Black hole thermodynamics and Black hole information paradox. Quantum theoryHirschman showed in 1957, however, that Heisenberg's uncertainty principle can be expressed as a particular lower bound on the sum of the entropies of the observable probability distributions of a particle's position and momentum, when they are expressed in Planck units. (One could speak of the "joint entropy" of these distributions by considering them independent, but since they are not jointly observable, they cannot be considered as a joint distribution.) It is well known that a Shannon based definition of information entropy leads in the classical case to the Boltzmann entropy. It is tempting to regard the Von Neumann entropy as the corresponding quantum mechanical definition. But the latter is problematic from quantum information point of view. Consequently Stotland, Pomeransky, Bachmat and Cohen have introduced a new definition of entropy that reflects the inherent uncertainty of quantum mechanical states. This definition allows to distinguish between the minimum uncertainty entropy of pure states, and the excess statistical entropy of mixtures.
The fluctuation theoremThe fluctuation theorem provides a mathematical justification of the second law of thermodynamics under these principles, and precisely defines the limitations of the applicability of that law to the microscopic realm of individual particle movements. Topics of recent researchIs information quantized?In 1995, Tim Palmer signalled two unwritten assumptions about Shannon's definition of information that may make it inapplicable as such to quantum mechanics:
The article Conceptual inadequacy of the Shannon information in quantum measurement [2], published in 2001 by Anton Zeilinger [3] and Caslav Brukner, synthesized and developed these remarks. The so-called Zeilinger's principle suggests that the quantization observed in QM could be bound to information quantization (one cannot observe less than one bit, and what is not observed is by definition "random"). But these claims remain highly controversial. For a detailed discussion of the applicability of the Shannon information in quantum mechanics and an argument that Zeilinger's principle cannot explain quantization, see Timpson [4] 2003 [5] and also Hall 2000 [6] and Mana 2004 [7] For a tutorial on quantum information see [8]. See also
References
|
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Entropy_in_thermodynamics_and_information_theory". A list of authors is available in Wikipedia. |





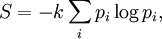
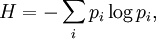
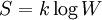
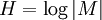
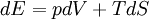
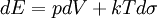
![H[f] = -\int_{-\infty}^{\infty} f(x) \log[ f(x)]\, dx,\quad](images/math/4/3/6/436dc6c75572f6935419a601aded0bcc.png)