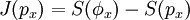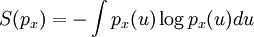Negentropy

In 1943 Erwin Schrödinger used the concept of “negative entropy” in his popular-science book What is life? ^[1]. Later, Léon Brillouin shortened the expression to a single word, negentropy. ^[2][3] Schrödinger introduced the concept when explaining that a living system exports entropy in order to maintain its own entropy at a low level (see entropy and life). By using the term negentropy, he could express this fact in a more "positive" way: a living system imports negentropy and stores it.

In a note to What is Life? Schrödinger explains his usage of this term.

In 1974, Albert Szent-Györgyi proposed replacing the term negentropy with syntropy, a term which may have originated in the 1940s with the Italian mathematician Luigi Fantappiè, who attempted to construct a unified theory of the biological and physical worlds. (This attempt has not gained renown or borne great fruit.) Buckminster Fuller attempted to popularize this usage, though negentropy still remains common.

Additional recommended knowledge

Recognize and detect the effects of electrostatic charges on your balance

Weighing the right way

How to quickly check pipettes?

Information theory

In information theory and statistics, negentropy is used as a measure of distance to normality. ^[4][5][6] Consider a signal with a certain distribution. If the signal is Gaussian, the signal is said to have a normal distribution. Negentropy is always positive, is invariant by any linear invertible change of coordinates, and vanishes iff the signal is Gaussian.

Negentropy is defined as

where S(φ_x) stands for the Gaussian density with the same mean and variance as p_x and S(p_x) is the differential entropy:

Negentropy is used in statistics and signal processing. It is related to network entropy, which is used in Independent Component Analysis. ^[7][8] Negentropy can be understood intuitively as the information that can be saved when representing p_x in an efficient way; if p_x where a random variable (with Gaussian distribution) with the same mean and variance, would need the maximum length of data to be represented, even in the most efficient way. Since p_x is less random, then something about it is known beforehand, it contains less unknown information, and needs less length of data to be represented in an efficient way.

Organization theory

In risk management, negentropy is the force that seeks to achieve effective organizational behavior and lead to a steady predictable state.^[9]

Notes

1. ^ Schrödinger Erwin What is Life - the Physical Aspect of the Living Cell, Cambridge University Press, 1944
2. ^ Brillouin, Leon: (1953) "Negentropy Principle of Information", /J. of Applied Physics/, v. 24:9, pp. 1152-1163
3. ^ Léon Brillouin La science et la théorie de l'information, Masson, 1959
4. ^ http://www.cis.hut.fi/aapo/papers/NCS99web/node32.html Aapo Hyvärinen, Survey on Independent Component Analysis, node32: Negentropy, Helsinki University of Technology Laboratory of Computer and Information Science
5. ^ http://www.cis.hut.fi/aapo/papers/IJCNN99_tutorialweb/node14.html Aapo Hyvärinen and Erkki Oja, Independent Component Analysis: A Tutorial, node14: Negentropy, Helsinki University of Technology Laboratory of Computer and Information Science
6. ^ Ruye Wang, Independent Component Analysis, node4: Measures of Non-Gaussianity
7. ^ P. Comon, Independent Component Analysis - a new concept?, Signal Processing, 36:287-314, 1994.
8. ^ http://www.fmrib.ox.ac.uk/analysis/techrep/tr01dl1/tr01dl1/tr01dl1.html Didier G. Leibovici and Christian Beckmann, An introduction to Multiway Methods for Multi-Subject fMRI experiment. FMRIB Technical Report, Oxford Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB), Department of Clinical Neurology, University of Oxford, John Radcliffe Hospital, Headley Way, Headington, Oxford, UK.
9. ^ Pedagogical Risk and Governmentality: Shantytowns in Argentina in the 21st Century (see p. 4).

See also

• Ectropy
• Exformation
• Extropy
• Free entropy
• Entropy in thermodynamics and information theory
• Entropy and life