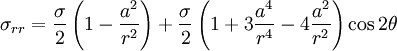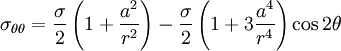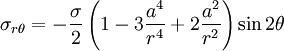My watch list

Kirsch equations

The Kirsch equations describe the elastic stresses around the hole in an infinite plate in one directional tension. They are named after Ernst Gustav Kirsch.

Additional recommended knowledge

Better weighing performance in 6 easy steps

Recognize and detect the effects of electrostatic charges on your balance

How to quickly check pipettes?

Result

Loading an infinite plate with circular hole of radius a with stress σ, the resulting stress field is:

$\sigma_{rr} = \frac{\sigma}{2}\left(1 - \frac{a^2}{r^2}\right) + \frac{\sigma}{2}\left(1 + 3\frac{a^4}{r^4} - 4\frac{a^2}{r^2}\right)\cos 2\theta$

$\sigma_{\theta\theta} = \frac{\sigma}{2}\left(1 + \frac{a^2}{r^2}\right) - \frac{\sigma}{2}\left(1 + 3\frac{a^4}{r^4}\right)\cos 2\theta$

$\sigma_{r\theta} = - \frac{\sigma}{2}\left(1 - 3\frac{a^4}{r^4} + 2\frac{a^2}{r^2}\right)\sin 2\theta$

References

Kirsch, 1898, Die Theorie der Elastizität und die Bedürfnisse der Festigkeitslehre. Zeitshrift des Vereines deutscher Ingenieure, 42, 797–807.

Category: Solid mechanics

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Kirsch_equations". A list of authors is available in Wikipedia.

The LUMITOS industry portals