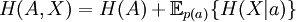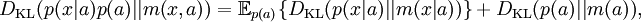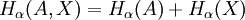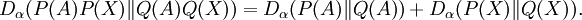To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rényi entropyIn information theory, the Rényi entropy, a generalisation of Shannon entropy, is one of a family of functionals for quantifying the diversity, uncertainty or randomness of a system. It is named after Alfréd Rényi. The Rényi entropy of order α, where α where pi are the probabilities of {x1, x2 ... xn}. If the probabilities are all the same then all the Rényi entropies of the distribution are equal, with Hα(X)=log n. Otherwise the entropies are weakly decreasing as a function of α. Some particular cases: which is the logarithm of the cardinality of X, sometimes called the Hartley entropy of X. In the limit that α approaches 1, it can be shown that Hα converges to which is the Shannon entropy. Sometimes Renyi entropy refers only to the case α = 2, where Y is a random variable independent of X but identically distributed to X. As and this is called Min-entropy, because it is smallest value of Hα. These two latter cases are related by The Rényi entropies are important in ecology and statistics as indices of diversity. They also lead to a spectrum of indices of fractal dimension. Product highlight
Rényi relative informationsAs well as the absolute Rényi entropies, Rényi also defined a spectrum of generalised relative information gains (the negative of relative entropies), generalising the Kullback–Leibler divergence. The Rényi generalised divergence of order α, where α > 0, of an approximate distribution or a prior distribution Q(x) from a "true" distribution or an updated distribution P(x) is defined to be: Like the Kullback-Leibler divergence, the Rényi generalised divergences are always non-negative. Some special cases:
Why α = 1 is specialThe value α = 1, which gives the Shannon entropy and the Kullback–Leibler divergence, is special because it is only when α=1 that one can separate out variables A and X from a joint probability distribution, and write: for the absolute entropies, and for the relative entropies. The latter in particular means that if we seek a distribution p(x,a) which minimises the divergence of some underlying prior measure m(x,a), and we acquire new information which only affects the distribution of a, then the distribution of p(x|a) remains m(x|a), unchanged. The other Rényi divergences satisfy the criteria of being positive and continuous; being invariant under 1-to-1 co-ordinate transformations; and of combining additively when A and X are independent, so that if p(A,X) = p(A)p(X), then and The stronger properties of the α = 1 quantities, which allow the definition of the conditional informations and mutual informations which are so important in communication theory, may be very important in other applications, or entirely unimportant, depending on those applications' requirements. ReferencesA. Rényi (1961). "On measures of information and entropy". Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability 1960: 547-561. See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rényi_entropy". A list of authors is available in Wikipedia. |


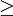 0, is defined as
0, is defined as
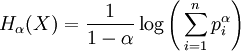
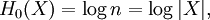
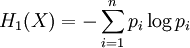
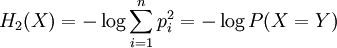
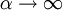 , the limit exists as
, the limit exists as
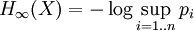
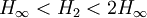 , while on the other hand Shannon entropy can be arbitrarily high for a random variable X with fixed min-entropy.
, while on the other hand Shannon entropy can be arbitrarily high for a random variable X with fixed min-entropy.



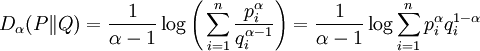
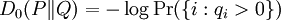 : minus the log probability that qi>0;
: minus the log probability that qi>0;
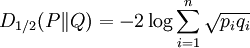 : minus twice the logarithm of the Bhattacharyya coefficient;
: minus twice the logarithm of the Bhattacharyya coefficient;
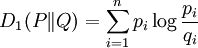 : the Kullback-Leibler divergence;
: the Kullback-Leibler divergence;
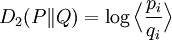 : the log of the expected ratio of the probabilities;
: the log of the expected ratio of the probabilities;
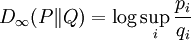 : the log of the maximum ratio of the probabilities.
: the log of the maximum ratio of the probabilities.