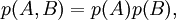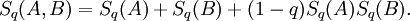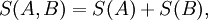To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Tsallis entropyIn physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. It was an extension put forward by Constantino Tsallis in 1988. It is defined as Product highlightor in the discrete case In this case, p denotes the probability distribution of interest, and q is a real parameter. In the limit as q → 1, the normal Boltzmann-Gibbs entropy is recovered. The parameter q is a measure of the non-extensitivity of the system of interest. There are continuous and discrete versions of this entropic measure. Various relationshipsThe discrete Tsallis entropy satisfies where Dq is the q-derivative. Non-extensivityGiven two independent systems A and B, for which the joint probability density satisfies the Tsallis entropy of this system satisfies From this result, it is evident that the parameter q is a measure of the departure from extensivity. In the limit when q = 1, which is what is expected for an extensive system. See alsoCategories: Entropy and information | Thermodynamic entropy |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Tsallis_entropy". A list of authors is available in Wikipedia. |


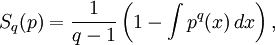



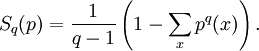
![S_q = - \left [ D_q \sum_i p_i^x \right ]_{x=1}](images/math/a/2/8/a283da3d9dbf5d0d7c0f30249edf1f78.png)