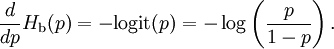To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Binary entropy function
Product highlightIn information theory, the binary entropy function, denoted If Pr(X = 1) = p, then Pr(X = 0) = 1 − p and the entropy of X is given by The logarithms in this formula are usually taken (as shown in the graph) to the base 2. See binary logarithm. When H(p) is distinguished from the entropy function by its taking a single scalar constant parameter. For tutorial purposes, in which the reader may not distinguish the appropriate function by its argument, H2(p) is often used; however, this could confuse this function with the analogous function related to Rényi entropy, so Hb(p) (with "b" not in italics) should be used to dispel ambiguity. DerivativeThe derivative of the binary entropy function may be expressed as the negative of the logit function: See also
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Binary_entropy_function". A list of authors is available in Wikipedia. |





 or
or  , is defined as the
, is defined as the 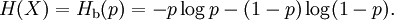
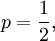 the binary entropy function attains its maximum value. This is the case of the unbiased bit, the most common unit of
the binary entropy function attains its maximum value. This is the case of the unbiased bit, the most common unit of