To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Self-informationIn information theory (elaborated by Claude E. Shannon, 1948), self-information is a measure of the information content associated with the outcome of a random variable. It is expressed in a unit of information, for example bits, nats, or hartleys (also known as digits, dits, bans), depending on the base of the logarithm used in its definition. Product highlightBy definition, the amount of self-information contained in a probabilistic event depends only on the probability of that event: the smaller its probability, the larger the self-information associated with receiving the information that the event indeed occurred. Further, by definition, the measure of self-information has the following property. If an event C is composed of two mutually independent events A and B, then the amount of information at the proclamation that C has happened, equals the sum of the amounts of information at proclamations of event A and event B respectively. Taking into account these properties, the self-information I(ωn) (measured in bits) associated with outcome ωn is: This definition, using the binary logarithm function, complies with the above conditions.
In the above definition, the logarithm of base 2 was used, and thus the unit of
This measure has also been called surprisal, as it represents the "surprise" of seeing the outcome (a highly probable outcome is not surprising). This term was coined by Myron Tribus in his 1961 book Thermostatics and Thermodynamics. The information entropy of a random event is the expected value of its self-information. Self-information is an example of a proper scoring rule. Examples
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Self-information". A list of authors is available in Wikipedia. |





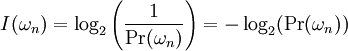
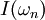 is in bit.
When using the logarithm of base
is in bit.
When using the logarithm of base 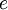 , the unit will be in
nat.
For the log of base 10, the unit will be in hartley.
, the unit will be in
nat.
For the log of base 10, the unit will be in hartley.


