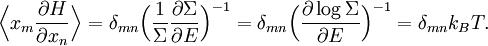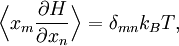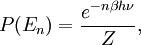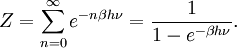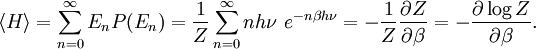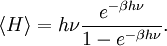To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Equipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among its various forms; for example, the average kinetic energy in the translational motion of a molecule should equal the average kinetic energy in its rotational motion. The equipartition theorem makes quantitative predictions. Like the virial theorem, it gives the total average kinetic and potential energies for a system at a given temperature, from which the system's heat capacity can be computed. However, equipartition also gives the average values of individual components of the energy, such as the kinetic energy of a particular particle or the potential energy of a single spring. For example, it predicts that every molecule in an ideal gas has an average kinetic energy of (3/2)kBT in thermal equilibrium, where kB is the Boltzmann constant and T is the temperature. More generally, it can be applied to any classical system in thermal equilibrium, no matter how complicated. The equipartition theorem can be used to derive the classical ideal gas law, and the Dulong–Petit law for the specific heat capacities of solids. It can also be used to predict the properties of stars, even white dwarfs and neutron stars, since it holds even when relativistic effects are considered. Although the equipartition theorem makes very accurate predictions in certain conditions, it becomes inaccurate when quantum effects are significant, namely at low enough temperatures. When the thermal energy kBT is smaller than the quantum energy spacing in a particular degree of freedom, the average energy and heat capacity of this degree of freedom are less than the values predicted by equipartition. Such a degree of freedom is said to be "frozen out" when the thermal energy is much smaller than this spacing. For example, the specific heat of a solid decreases at low temperatures as various types of motion become frozen out, rather than remaining constant as predicted by equipartition. Such decreases in specific heat were the first sign to physicists of the 19th century that classical physics was incorrect and that new physics was needed. Along with other evidence, equipartition's failure for electromagnetic radiation — also known as the ultraviolet catastrophe — led Albert Einstein to suggest that light itself was quantized into photons, a revolutionary hypothesis that spurred the development of quantum mechanics and quantum field theory. Product highlight
Basic concept and simple examples
The name "equipartition" means "share and share alike". The original concept of equipartition was that the total kinetic energy of a system is shared equally among all of its independent parts, on the average, once the system has reached thermal equilibrium. Equipartition also makes quantitative predictions for these energies. For example, it predicts that every atom of a noble gas, in thermal equilibrium at temperature T, has an average translational kinetic energy of (3/2)kBT, where kB is the Boltzmann constant. As a consequence, the heavier atoms of xenon have a lower average speed than do the lighter atoms of helium at the same temperature. Figure 2 shows the Maxwell–Boltzmann distribution for the speeds of the atoms in four noble gases. In this example, the key point is that the kinetic energy is quadratic in the velocity. The equipartition theorem shows that in thermal equilibrium, any degree of freedom (such as a component of the position or velocity of a particle) which appears only quadratically in the energy has an average energy of ½kBT and therefore contributes ½kB to the system's heat capacity. This has many applications. Translational energy and ideal gases
The (Newtonian) kinetic energy of a particle of mass m, velocity v is given by where vx, vy and vz are the cartesian components of the velocity v. Here, H is short for Hamiltonian, and used henceforth as a symbol for energy because the Hamiltonian formalism plays a central role in the most general form of the equipartition theorem. Since the kinetic energy is quadratic in the components of the velocity, by equipartition these three components each contribute ½kBT to the average kinetic energy in thermal equilibrium. Thus the average kinetic energy of the particle is (3/2)kBT, as in the example of noble gases above. More generally, in an ideal gas, the total energy consists purely of (translational) kinetic energy: by assumption, the particles have no internal degrees of freedom and move independently of one another. Equipartition therefore predicts that the average total energy of an ideal gas of N particles is (3/2) N kBT. It follows that the heat capacity of the gas is (3/2) N kB and hence, in particular, the heat capacity of a mole of a such gas particles is (3/2)NAkB=(3/2)R, where NA is Avogadro's number and R is the gas constant. Since R ≈ 2 cal/(mol·K), equipartition predicts that the molar heat capacity of an ideal gas is roughly 3 cal/(mol·K). This prediction is confirmed by experiment.[1] The mean kinetic energy also allows the root mean square speed vrms of the gas particles to be calculated: where M = NAm is the mass of a mole of gas particles. This result is useful for many applications such as Graham's law of effusion, which provides a method for enriching uranium.[2] Rotational energy and molecular tumbling in solution
A similar example is provided by a rotating molecule with principal moments of inertia I1, I2 and I3. The rotational energy of such a molecule is given by where ω1, ω2, and ω3 are the principal components of the angular velocity. By exactly the same reasoning as in the translational case, equipartition implies that in thermal equilibrium the average rotational energy of each particle is (3/2)kBT. Similarly, the equipartition theorem allows the average (more precisely, the root mean square) angular speed of the molecules to be calculated.[3] The tumbling of rigid molecules — that is, the random rotations of molecules in solution — plays a key role in the relaxations observed by nuclear magnetic resonance, particularly protein NMR and residual dipolar couplings.[4] Rotational diffusion can also be observed by other biophysical probes such as fluorescence anisotropy, flow birefringence and dielectric spectroscopy.[5] Potential energy and harmonic oscillatorsEquipartition applies to potential energies as well as kinetic energies: important examples include harmonic oscillators such as a spring, which has a quadratic potential energy where the constant a describes the stiffness of the spring and q is the deviation from equilibrium. If such a one dimensional system has mass m, then its kinetic energy Hkin is ½mv2 = p2/2m, where v and p = mv denote the velocity and momentum of the oscillator. Combining these terms yields the total energy[6] Equipartition therefore implies that in thermal equilibrium, the oscillator has average energy where the angular brackets This result is valid for any type of harmonic oscillator, such as a pendulum, a vibrating molecule or a passive electronic oscillator. Systems of such oscillators arise in many situations; by equipartition, each such oscillator receives an average total energy kBT and hence contributes kB to the system's heat capacity. This can be used to derive the formula for Johnson–Nyquist noise[8] and the Dulong–Petit law of solid molar heat capacities. The latter application was particularly significant in the history of equipartition.
Specific heat capacity of solids
An important application of the equipartition theorem is to the specific heat capacity of a crystalline solid. Each atom in such a solid can oscillate in three independent directions, so the solid can be viewed as a system of 3N independent simple harmonic oscillators, where N denotes the number of atoms in the lattice. Since each harmonic oscillator has average energy kBT, the average total energy of the solid is 3NkBT, and its heat capacity is 3NkB. By taking N to be Avogadro's number NA, and using the relation R = NAkB between the gas constant R and the Boltzmann constant kB, this provides an explanation for the Dulong–Petit law of molar heat capacities of solids, which states that the heat capacity per mole of atoms in the lattice is 3R ≈ 6 cal/(mol·K). However, this law is inaccurate at lower temperatures, due to quantum effects; it is also inconsistent with the experimentally derived third law of thermodynamics, according to which the molar heat capacity of any substance must go to zero as the temperature goes to absolute zero.[8] A more accurate theory, incorporating quantum effects, was developed by Albert Einstein (1907) and Peter Debye (1911).[9] Many other physical systems can be modeled as sets of coupled oscillators. The motions of such oscillators can be decomposed into normal modes, like the vibrational modes of a piano string or the resonances of an organ pipe. On the other hand, equipartition often breaks down for such systems, because there is no exchange of energy between the normal modes. In an extreme situation, the modes are independent and so their energies are independently conserved. This shows that some sort of mixing of energies, formally called ergodicity, is important for the law of equipartition to hold. Sedimentation of particles
Potential energies are not always quadratic in the position. However, the equipartition theorem also shows that if a degree of freedom x contributes only a multiple of xs (for a fixed real number s) to the energy, then in thermal equilibrium the average energy of that part is kBT/s. There is a simple application of this extension to the sedimentation of particles under gravity.[10] For example, the haze sometimes seen in beer can be caused by clumps of proteins that scatter light.[11] Over time, these clumps settle downwards under the influence of gravity, causing more haze near the bottom of a bottle than near its top. However, in a process working in the opposite direction, the particles also diffuse back up towards the top of the bottle. Once equilibrium has been reached, the equipartition theorem may be used to determine the average position of a particular clump of buoyant mass mb. For an infinitely tall bottle of beer, the gravitational potential energy is given by where z is the height of the protein clump in the bottle and g is the acceleration caused by gravity. Since s=1, the average potential energy of a protein clump equals kBT. Hence, a protein clump with a buoyant mass of 10 MDa (roughly the size of a virus) would produce a haze with an average height of about 2 cm at equilibrium. The process of such sedimentation to equilibrium is described by the Mason–Weaver equation.[12] History
The equipartition of kinetic energy was proposed initially in 1843, and more correctly in 1845, by John James Waterston.[13] In 1859, James Clerk Maxwell argued that the kinetic heat energy of a gas is equally divided between linear and rotational energy.[14] In 1876, Ludwig Boltzmann expanded on this principle by showing that the average energy was divided equally among all the independent components of motion in a system.[15][16] Boltzmann applied the equipartition theorem to provide a theoretical explanation of the Dulong–Petit law for the specific heat capacities of solids.
The history of the equipartition theorem is intertwined with that of molar heat capacity, both of which were studied in the 19th century. In 1819, the French physicists Pierre Louis Dulong and Alexis Thérèse Petit discovered that the molar-specific heats of solids at room temperature were almost all identical, roughly 6 cal/(mol·K).[18] Their law was used for many years as a technique for measuring atomic weights.[9] However, subsequent studies by James Dewar and Heinrich Friedrich Weber showed that this Dulong–Petit law holds only at high temperatures;[19] at lower temperatures, or for exceptionally hard solids such as diamond, the specific heat was lower.[20] Experimental observations of the specific heat of gases also raised concerns about the validity of the equipartition theorem. The theorem predicts that the molar heat capacity of simple monatomic gases should be roughly 3 cal/(mole·K), whereas that of diatomic gases should be roughly 7 cal/(mol·K). Experiments confirmed the former prediction,[1] but found that molar heat capacities of diatomic gases were typically about 5 cal/(mol·K),[21] and fell to about 3 cal/(mol·K) at very low temperatures.[22] Maxwell noted in 1875 that the disagreement between experiment and the equipartition theorem was much worse than even these numbers suggest;[23] since atoms have internal parts, heat energy should go into the motion of these internal parts, making the predicted specific heats of monatomic and diatomic gases much higher than 3 cal/(mol·K) and 7 cal/(mol·K), respectively. A third discrepancy concerned the specific heat of metals.[24] According to the classical Drude model, metallic electrons act as a nearly ideal gas, and so they should contribute (3/2) Ne kB to the heat capacity by the equipartition theorem, where Ne is the number of electrons. Experimentally, however, electrons contribute little to the heat capacity: the molar heat capacities of many conductors and insulators are nearly the same.[24] Several explanations of equipartition's failure to account for molar heat capacities were proposed. Boltzmann defended the derivation of his equipartition theorem as correct, but suggested that gases might not be in thermal equilibrium because of their interactions with the aether.[25] Lord Kelvin suggested that the derivation of the equipartition theorem must be incorrect, since it disagreed with experiment, but was unable to show how.[26] Lord Rayleigh instead put forward a more radical view that the equipartition theorem and the experimental assumption of thermal equilibrium were both correct; to reconcile them, he noted the need for a new principle that would provide an "escape from the destructive simplicity" of the equipartition theorem.[27] Albert Einstein provided that escape, by showing in 1907 that these anomalies in the specific heat were due to quantum effects, specifically the quantization of energy in the elastic modes of the solid.[28] Einstein used the failure of equipartition to argue for the need of a new quantum theory of matter.[9] Nernst's 1910 measurements of specific heats at low temperatures[29] supported Einstein's theory, and led to the widespread acceptance of quantum theory among physicists.[30] General formulation of the equipartition theorem
The most general form of the equipartition theorem[10][7][3] states that under suitable assumptions (discussed below), for a physical system with Hamiltonian energy function H and degrees of freedom xn, the following equipartition formula holds in thermal equilibrium for all indices m and n: Here δmn is the Kronecker delta, which is equal to one if m=n and is zero otherwise. The averaging brackets The general equipartition theorem holds in both the microcanonical ensemble,[7] when the total energy of the system is constant, and also in the canonical ensemble,[31][3] when the system is coupled to a heat bath with which it can exchange energy. Derivations of the general formula are given later in the article. The general formula is equivalent to the following two.
If a degree of freedom xn appears only as a quadratic term anxn2 in the Hamiltonian H, then the first of these formulae implies that which is twice the contribution that this degree of freedom makes to the average energy The degrees of freedom xn are coordinates on the phase space of the system and are therefore commonly subdivided into generalized position coordinates qk and generalized momentum coordinates pk, where pk is the conjugate momentum to qk. In this situation, formula 1 means that for all k, Using the equations of Hamiltonian mechanics,[6] these formulae may also be written Formula 2 additionally states that the averages
are all zero for j≠k. Relation to the virial theorem
The general equipartition theorem is an extension of the virial theorem (proposed in 1870[32]), which states that where t denotes time.[6] Two key differences are that the virial theorem relates summed rather than individual averages to each other, and it does not connect them to the temperature T. Another difference is that traditional derivations of the virial theorem use averages over time, whereas those of the equipartition theorem use averages over phase space. ApplicationsIdeal gas law
Ideal gases provide an important application of the equipartition theorem. As well as providing the formula for the average kinetic energy per particle, the equipartition theorem can be used to derive the ideal gas law from classical mechanics.[3] If q = (qx, qy, qz) and p = (px, py, pz) denote the position vector and momentum of a particle in the gas, and F is the net force on that particle, then where the first equality is Newton's second law, and the second line uses Hamilton's equations and the equipartition formula. Summing over a system of N particles yields
By Newton's third law and the ideal gas assumption, the net force on the system is the force applied by the walls of their container, and this force is given by the pressure P of the gas. Hence where dS is the infinitesimal area element along the walls of the container. Since the divergence of the position vector q is the divergence theorem implies that where dV is an infinitesimal volume within the container and V is the total volume of the container. Putting these equalities together yields which immediately implies the ideal gas law for N particles: where n=N/NA is the number of moles of gas and R=NAkB is the gas constant. Diatomic gases
A diatomic gas can be modelled as two masses, m1 and m2, joined by a spring of stiffness a, which is called the rigid rotor-harmonic oscillator approximation.[17] The classical energy of this system is where p1 and p2 are the momenta of the two atoms, and q is the deviation of the inter-atomic separation from its equilibrium value. Every degree of freedom in the energy is quadratic and, thus, should contribute ½kBT to the total average energy, and ½kB to the heat capacity. Therefore, the heat capacity of a gas of N diatomic molecules is predicted to be 7N · ½kB: the momenta p1 and p2 contribute three degrees of freedom each, and the extension q contributes the seventh. It follows that the heat capacity of a mole of diatomic molecules with no other degrees of freedom should be (7/2)NAkB=(7/2)R and, thus, the predicted molar heat capacity should be roughly 7 cal/(mol·K). However, the experimental values for molar heat capacities of diatomic gases are typically about 5 cal/(mol·K)[21] and fall to 3 cal/(mol·K) at very low temperatures.[22] This disagreement between the equipartition prediction and the experimental value of the molar heat capacity cannot be explained by using a more complex model of the molecule, since adding more degrees of freedom can only increase the predicted specific heat, not decrease it.[23] This discrepancy was a key piece of evidence showing the need for a quantum theory of matter.
Extreme relativistic ideal gases
Equipartition was used above to derive the classical ideal gas law from Newtonian mechanics. However, relativistic effects become dominant in some systems, such as white dwarfs and neutron stars,[7] and the ideal gas equations must be modified. The equipartition theorem provides a convenient way to derive the corresponding laws for an extreme relativistic ideal gas.[3] In such cases, the kinetic energy of a single particle is given by the formula Taking the derivative of H with respect to the px momentum component gives the formula and similarly for the py and pz components. Adding the three components together gives where the last equality follows from the equipartition formula. Thus, the average total energy of an extreme relativistic gas is twice that of the non-relativistic case: for N particles, it is 3 N kBT. Non-ideal gases
In an ideal gas the particles are assumed to interact only through collisions. The equipartition theorem may also be used to derive the energy and pressure of "non-ideal gases" in which the particles also interact with one another through conservative forces whose potential U(r) depends only on the distance r between the particles.[3] This situation can be described by first restricting attention to a single gas particle, and approximating the rest of the gas by a spherically symmetric distribution. It is then customary to introduce a radial distribution function g(r) such that the probability density of finding another particle at a distance r from the given particle is equal to 4πr2ρ g(r), where ρ=N/V is the mean density of the gas.[33] It follows that the mean potential energy associated to the interaction of the given particle with the rest of the gas is The total mean potential energy of the gas is therefore A similar argument,[3] can be used to derive the pressure equation Anharmonic oscillators
An anharmonic oscillator (in contrast to a simple harmonic oscillator) is one in which the potential energy is not quadratic in the extension q (the generalized position which measures the deviation of the system from equilibrium). Such oscillators provide a complementary point of view on the equipartition theorem.[34][35] Simple examples are provided by potential energy functions of the form where C and s are arbitrary real constants. In these cases, the law of equipartition predicts that Thus, the average potential energy equals kBT/s, not kBT/2 as for the quadratic harmonic oscillator (where s=2). More generally, a typical energy function of a one-dimensional system has a Taylor expansion in the extension q: for non-negative integers n. There is no n=1 term, because at the equilibrium point, there is no net force and so the first derivative of the energy is zero. The n=0 term need not be included, since the energy at the equilibrium position may be set to zero by convention. In this case, the law of equipartition predicts that[34] In contrast to the other examples cited here, the equipartition formula does not allow the average potential energy to be written in terms of known constants. Brownian motion
The equipartition theorem can be used to derive the Brownian motion of a particle from the Langevin equation.[3] According to that equation, the motion of a particle of mass m with velocity v is governed by Newton's second law where Frnd is a random force representing the random collisions of the particle and the surrounding molecules, and where the time constant τ reflects the drag force that opposes the particle's motion through the solution. The drag force is often written Fdrag = - γv; therefore, the time constant τ equals m/γ. The dot product of this equation with the position vector r, after averaging, yields the equation for Brownian motion (since the random force Frnd is uncorrelated with the position r). Using the mathematical identities and the basic equation for Brownian motion can be transformed into where the last equality follows from the equipartition theorem for translational kinetic energy: The above differential equation for On small time scales, with t << τ, the particle acts as a freely moving particle: by the Taylor series of the exponential function, the squared distance grows approximately quadratically: However, on long time scales, with t >> τ, the exponential and constant terms are negligible, and the squared distance grows only linearly: This describes the diffusion of the particle over time. An analogous equation for the rotational diffusion of a rigid molecule can be derived in a similar way.
Stellar physics
The equipartition theorem and the related virial theorem have long been used as a tool in astrophysics.[36] As examples, the virial theorem may be used to estimate stellar temperatures or the Chandrasekhar limit on the mass of white dwarf stars.[37][38] The average temperature of a star can be estimated from the equipartition theorem.[39] Since most stars are spherically symmetric, the total gravitational potential energy can be estimated by integration where M(r) is the mass within a radius r and ρ(r) is the stellar density at radius r; G represents the gravitational constant and R the total radius of the star. Assuming a constant density throughout the star, this integration yields the formula where M is the star's total mass. Hence, the average potential energy of a single particle is where N is the number of particles in the star. Since most stars are composed mainly of ionized hydrogen, N equals roughly (M/mp), where mp is the mass of one proton. Application of the equipartition theorem gives an estimate of the star's temperature Substitution of the mass and radius of the Sun yields an estimated solar temperature of T = 14 million kelvins, very close to its core temperature of 15 million kelvins. However, the Sun is much more complex than assumed by this model — both its temperature and density vary strongly with radius — and such excellent agreement (≈7% relative error) is partly fortuitous.[40] Star formationThe same formulae may be applied to determining the conditions for star formation in giant molecular clouds.[41] A local fluctuation in the density of such a cloud can lead to a runaway condition in which the cloud collapses inwards under its own gravity. Such a collapse occurs when the equipartition theorem — or, equivalently, the virial theorem — is no longer valid, i.e., when the gravitational potential energy exceeds twice the kinetic energy Assuming a constant density ρ for the cloud yields a minimum mass for stellar contraction, the Jeans mass MJ Substituting the values typically observed in such clouds (T=150 K, ρ = 2×10-16 g/cm3) gives an estimated minimum mass of 17 solar masses, which is consistent with observed star formation. This effect is also known as the Jeans instability, after the British physicist James Hopwood Jeans who published it in 1902.[42] DerivationsKinetic energies and the Maxwell–Boltzmann distributionThe original formulation of the equipartition theorem states that, in any physical system in thermal equilibrium, every particle has exactly the same average kinetic energy, (3/2)kBT.[43] This may be shown using the Maxwell–Boltzmann distribution (see Figure 2), which is the probability distribution for the speed of a particle of mass m in the system, where the speed v is the magnitude The Maxwell–Boltzmann distribution applies to any system composed of atoms, and assumes only a canonical ensemble, specifically, that the kinetic energies are distributed according to their Boltzmann factor at a temperature T.[43] The average kinetic energy for a particle of mass m is then given by the integral formula as stated by the equipartition theorem. Quadratic energies and the partition functionMore generally, the equipartition theorem states that any degree of freedom x which appears in the total energy H only as a simple quadratic term Ax2, where A is a constant, has an average energy of ½kBT in thermal equilibrium. In this case the equipartition theorem may be derived from the partition function Z(β), where β=1/(kBT) is the canonical inverse temperature.[44] Integration over the variable x yields a factor in the formula for Z. The mean energy associated with this factor is given by as stated by the equipartition theorem. General proofsGeneral derivations of the equipartition theorem can be found in many statistical mechanics textbooks, both for the microcanonical ensemble[7][3] and for the canonical ensemble.[31][3] They involve taking averages over the phase space of the system, which is a symplectic manifold. To explain these derivations, the following notation is introduced. First, the phase space is described in terms of generalized position coordinates qj together with their conjugate momenta pj. The quantities qj completely describe the configuration of the system, while the quantities (qj,pj) together completely describe its state. Secondly, the infinitesimal volume
of the phase space is introduced and used to define the volume Γ(E, ΔE) of the portion of phase space where the energy H of the system lies between two limits, E and E+ΔE: In this expression, ΔE is assumed to be very small, ΔE<
Since ΔE is very small, the following integrations are equivalent where the ellipses represent the integrand. From this, it follows that Γ is proportional to ΔE where ρ(E) is the density of states. By the usual definitions of statistical mechanics, the entropy S equals kB log Σ(E), and the temperature T is defined by The canonical ensembleIn the canonical ensemble, the system is in thermal equilibrium with an infinite heat bath at temperature T (in Kelvin).[31][3] The probability of each state in phase space is given by its Boltzmann factor times a normalization factor where β = 1/kBT. Integration by parts for a phase-space variable xk (which could be either qk or pk) between two limits a and b yields the equation where dΓk = dΓ/dxk, i.e., the first integration is not carried out over xk. The first term is usually zero, either because xk is zero at the limits, or because the energy goes to infinity at those limits. In that case, the equipartition theorem for the canonical ensemble follows immediately Here, the averaging symbolized by The microcanonical ensembleIn the microcanonical ensemble, the system is isolated from the rest of the world, or at least very weakly coupled to it.[7] Hence, its total energy is effectively constant; to be definite, we say that the total energy H is confined between E and E+ΔE. For a given energy E and spread ΔE, there is a region of phase space Γ in which the system has that energy, and the probability of each state in that region of phase space is equal, by the definition of the microcanonical ensemble. Given these definitions, the equipartition average of phase-space variables xm (which could be either qkor pk) and xn is given by where the last equality follows because E is a constant that does not depend on xn. Integrating by parts yields the relation since the first term on the right hand side of the first line is zero (it can be rewritten as an integral of H - E on the hypersurface where H = E). Substitution of this result into the previous equation yields Since Thus, we have derived the general formulation of the equipartition theorem which was so useful in the applications described above. Limitations
Requirement of ergodicity
The law of equipartition holds only for ergodic systems in thermal equilibrium, which implies that all states with the same energy must be equally likely to be populated.[7] Consequently, it must be possible to exchange energy among all its various forms within the system, or with an external heat bath in the canonical ensemble. The number of physical systems that have been rigorously proven to be ergodic is small; a famous example is the hard-sphere system of Yakov Sinai.[45] The requirements for isolated systems to ensure ergodicity — and, thus equipartition — have been studied, and provided motivation for the modern chaos theory of dynamical systems. A chaotic Hamiltonian system need not be ergodic, although that is usually a good assumption.[46] A commonly cited counter-example where energy is not shared among its various forms and where equipartition does not hold in the microcanonical ensemble is a system of coupled harmonic oscillators.[46] If the system is isolated from the rest of the world, the energy in each normal mode is constant; energy is not transferred from one mode to another. Hence, equipartition does not hold for such a system; the amount of energy in each normal mode is fixed at its initial value. If sufficiently strong nonlinear terms are present in the energy function, energy may be transferred between the normal modes, leading to ergodicity and rendering the law of equipartition valid. However, the Kolmogorov–Arnold–Moser theorem states that energy will not be exchanged unless the nonlinear perturbations are strong enough; if they are too small, the energy will remain trapped in at least some of the modes. Failure due to quantum effects
The law of equipartition breaks down when the thermal energy kBT is significantly smaller than the spacing between energy levels. Equipartition no longer holds because it is a poor approximation to assume that the energy levels form a smooth continuum, which is required in the derivations of the equipartition theorem above.[7][3] Historically, the failures of the classical equipartition theorem to explain specific heats and blackbody radiation were critical in showing the need for a new theory of matter and radiation, namely, quantum mechanics and quantum field theory.[9]
To illustrate the breakdown of equipartition, consider the average energy in a single (quantum) harmonic oscillator, which was discussed above for the classical case. Its quantum energy levels are given by En = nhν, where h is Planck's constant, ν is the fundamental frequency of the oscillator, and n is an integer. The probability of a given energy level being populated in the canonical ensemble is given by its Boltzmann factor where β = 1/kBT and the denominator Z is the partition function, here a geometric series Its average energy is given by Substituting the formula for Z gives the final result[7] At high temperatures, when the thermal energy kBT is much greater than the spacing hν between energy levels, the exponential argument βhν is much less than one and the average energy becomes kBT, in agreement with the equipartition theorem (Figure 10). However, at low temperatures, when hν >> kBT, the average energy goes to zero — the higher-frequency energy levels are "frozen out" (Figure 10). As another example, the internal excited electronic states of a hydrogen atom do not contribute to its specific heat as a gas at room temperature, since the thermal energy kBT (roughly 0.025 eV) is much smaller than the spacing between the lowest and next higher electronic energy levels (roughly 10 eV). Similar considerations apply whenever the energy level spacing is much larger than the thermal energy. For example, this reasoning was used by Albert Einstein to resolve the ultraviolet catastrophe of blackbody radiation.[47] The paradox arises because there are an infinite number of independent modes of the electromagnetic field in a closed container, each of which may be treated as a harmonic oscillator. If each electromagnetic mode were to have an average energy kBT, there would be an infinite amount of energy in the container.[47][48] However, by the reasoning above, the average energy in the higher-ω modes goes to zero as ω goes to infinity; moreover, Planck's law of black body radiation, which describes the experimental distribution of energy in the modes, follows from the same reasoning.[47] Other, more subtle quantum effects can lead to corrections to equipartition, such as identical particles and continuous symmetries. The effects of identical particles can be dominant at very high densities and low temperatures. For example, the valence electrons in a metal can have a mean kinetic energy of a few electronvolts, which would normally correspond to a temperature of tens of thousands of kelvins. Such a state, in which the density is high enough that the Pauli exclusion principle invalidates the classical approach, is called a degenerate fermion gas. Such gases are important for the structure of white dwarf and nuetron stars. At low temperatures, a fermionic analogue of the Bose–Einstein condensate (in which a large number of identical particles occupy the lowest-energy state) can form; such superfluid electrons are responsible for superconductivity. See alsoNotes and references
Further reading
Categories: Statistical mechanics | Thermodynamics |
|||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Equipartition_theorem". A list of authors is available in Wikipedia. |





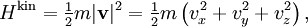
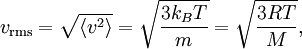
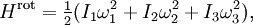
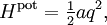
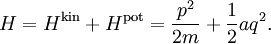
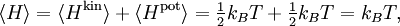
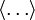 denote the average of the enclosed quantity,
denote the average of the enclosed quantity,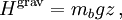
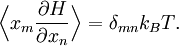
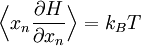 for all n.
for all n.
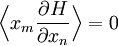 for all m≠n.
for all m≠n.
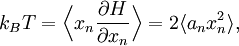
 . Thus the equipartition theorem for systems with quadratic energies follows easily from the general formula. A similar argument, with 2 replaced by s, applies to energies of the form anxns.
. Thus the equipartition theorem for systems with quadratic energies follows easily from the general formula. A similar argument, with 2 replaced by s, applies to energies of the form anxns.
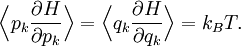
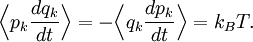
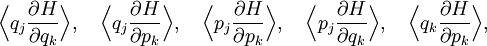 and
and 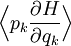
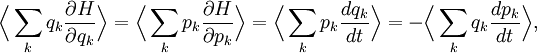
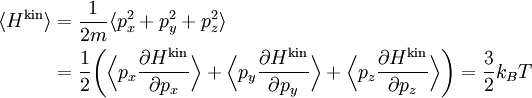
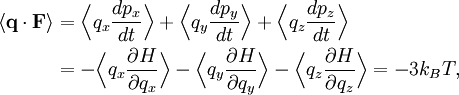
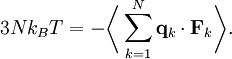
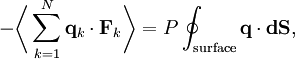
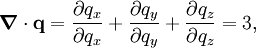
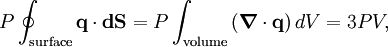
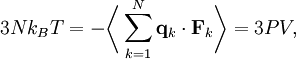
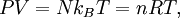
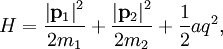
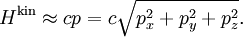
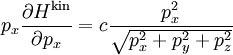
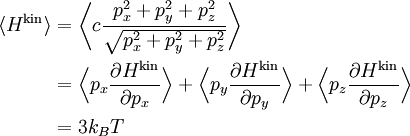
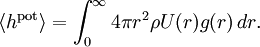
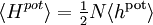 , where N is the number of particles in the gas, and the factor ½ is needed because summation over all the particles counts each interaction twice.
Adding kinetic and potential energies, then applying equipartition, yields the energy equation
, where N is the number of particles in the gas, and the factor ½ is needed because summation over all the particles counts each interaction twice.
Adding kinetic and potential energies, then applying equipartition, yields the energy equation
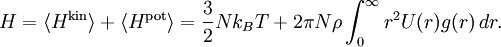
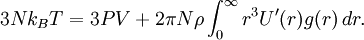
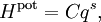
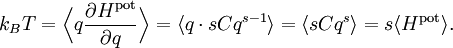
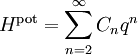
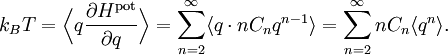
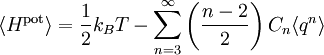
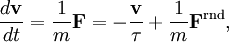
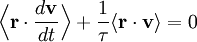
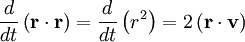
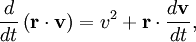
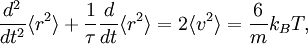
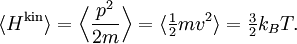
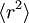 (with suitable initial conditions) may be solved exactly:
(with suitable initial conditions) may be solved exactly:
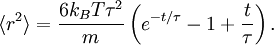
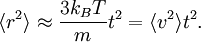
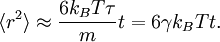
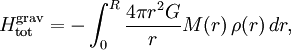
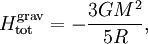
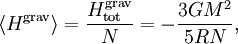
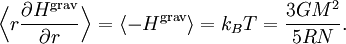
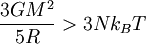
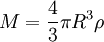
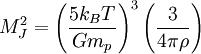
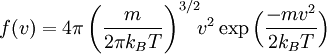
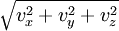 of the velocity vector
of the velocity vector 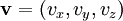 .
.
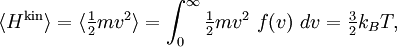
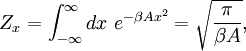
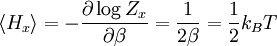
![\Gamma (E, \Delta E) = \int_{H \in \left[E, E+\Delta E \right]} d\Gamma .](images/math/8/2/7/8271c8ebb7932467732895190cf75e2c.png)
![\int_{H \in \left[ E, E+\Delta E \right]} \ldots d\Gamma = \Delta E \frac{\partial}{\partial E} \int_{H < E} \ldots d\Gamma,](images/math/7/b/c/7bc53bad3dc34d9f27e63dab50234805.png)
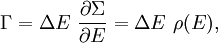
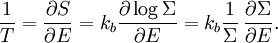
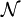 , which is chosen so that the probabilities sum to one
, which is chosen so that the probabilities sum to one
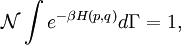
![\mathcal{N} \int \left[ e^{-\beta H(p, q)} x_{k} \right]_{x_{k}=a}^{x_{k}=b} d\Gamma_{k}+ \mathcal{N} \int e^{-\beta H(p, q)} x_{k} \beta \frac{\partial H}{\partial x_{k}} d\Gamma = 1,](images/math/b/e/8/be8c97969d4fb474e30a9daa818f4327.png)
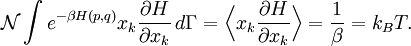
 is the
is the ![\begin{align} \Bigl\langle x_{m} \frac{\partial H}{\partial x_{n}} \Bigr \rangle &= \frac{1}{\Gamma} \, \int_{H \in \left[ E, E+\Delta E \right]} x_{m} \frac{\partial H}{\partial x_{n}} \,d\Gamma\\ &=\frac{\Delta E}{\Gamma}\, \frac{\partial}{\partial E} \int_{H < E} x_{m} \frac{\partial H}{\partial x_{n}} \,d\Gamma\\ &= \frac{1}{\rho} \,\frac{\partial}{\partial E} \int_{H < E} x_{m} \frac{\partial \left( H - E \right)}{\partial x_{n}} \,d\Gamma, \end{align}](images/math/1/7/1/171896bd98721d798bad87d4a7eec7e6.png)
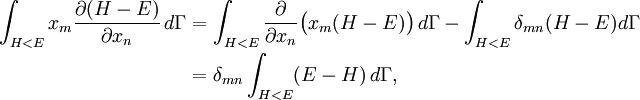
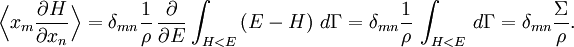
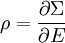 the equipartition theorem follows:
the equipartition theorem follows: