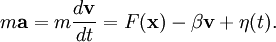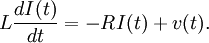To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Langevin equationIn statistical physics, a Langevin equation is a stochastic differential equation describing Brownian motion in a potential. Product highlightThe first Langevin equations to be studied were those in which the potential is constant, so that the acceleration a of a Brownian particle of mass m is expressed as the sum of a viscous force which is proportional to the particles velocity v (Stokes' law), a noise term Essentially similar equations govern other Brownian systems, such as thermal noise in an electrical resistor: Many interesting results can often be obtained without solving the Langevin equation, from the fluctuation dissipation theorem. The main method of solution if a solution is required is by use of the Fokker-Planck equation, which provides a deterministic equation satisfied by the time dependent probability density. Alternatively numerical solutions can be obtained by Monte Carlo simulation. Other techniques, such as path integration have also been used, drawing on the analogy between statistical physics and quantum mechanics (for example the Fokker-Planck equation can be transformed into the Schrödinger equation by rescaling a few variables). Further reading
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Langevin_equation". A list of authors is available in Wikipedia. |





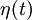 (the name given in physical contexts to terms in stochastic differential equations which are stochastic processes) representing the effect of a continuous series of collisions with the atoms of the underlying fluid and
(the name given in physical contexts to terms in stochastic differential equations which are stochastic processes) representing the effect of a continuous series of collisions with the atoms of the underlying fluid and