To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Debye modelIn thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912[1] for estimating the phonon contribution to the specific heat (heat capacity) in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box, in contrast to Einstein model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low temperature dependence of the heat capacity, which is proportional to T3. Just like the Einstein model, it also recovers the Dulong-Petit law at high temperatures. But due to simplifying assumptions, its accuracy suffers at intermediate temperatures. Product highlight
DerivationThe Debye model is a solid-state equivalent of Planck's law of black body radiation, where one treats electromagnetic radiation as a gas of photons in a box. The Debye model treats atomic vibrations as phonons in a box (the box being the solid). Most of the calculation steps are identical. Consider a cube of side L. From the particle in a box article, the resonating modes of the sonic disturbances inside the box (considering for now only those aligned with one axis) have wavelengths given by where n is an integer. The energy of a phonon is where h is Planck's constant and νn is the frequency of the phonon. We make the approximation that the frequency is inversely proportional to the wavelength, giving: in which cs is the speed of sound inside the solid. In three dimensions we will use: The approximation that the frequency is inversely proportional to the wavelength (giving a constant speed of sound) is good for low-energy phonons but not for high-energy phonons. (See the article on phonons.) This is one of the limitations of the Debye model. Let's now compute the total energy in the box where Now, this is where Debye model and Planck's law of black body radiation differ. Unlike electromagnetic radiation in a box, there is a finite number of phonon energy states because a phonon cannot have infinite frequency. Its frequency is bound by the medium of its propagation -- the atomic lattice of the solid. Consider an illustration of a transverse phonon below. It is reasonable to assume that the minimum wavelength of a phonon is twice the atom separation, as shown in the lower figure. There are N atoms in a solid. Our solid is a cube, which means there are making the maximum mode number n (infinite for photons) This is the upper limit of the triple energy sum For slowly-varying, well-behaved functions, a sum can be replaced with an integral (also known as Thomas-Fermi approximation) So far, there has been no mention of Because a phonon has three possible polarization states (one longitudinal and two transverse) which do not affect its energy, the formula above must be multiplied by 3 Substituting this into the energy integral yields The ease with which these integrals are evaluated for photons is due to the fact that light's frequency, at least semi-classically, is unbound. As the figure above illustrates, this is not true for phonons. In order to approximate this triple integral, Debye used spherical coordinates and boldly approximated the cube by an eighth of a sphere where R is the radius of this sphere, which is found by conserving the number of particles in the cube and in the eighth of a sphere. The volume of the cube is N unit-cell volumes, so we get: The substitution of integration over a sphere for the correct integral introduces another source of inaccuracy into the model. The energy integral becomes Changing the integration variable to To simplify the look of this expression, define the Debye temperature TD -- a shorthand for some constants and material-dependent variables. We then have the specific internal energy: where D3(x) is the (third) Debye function. Differentiating with respect to T we get the dimensionless heat capacity: These formulae give the Debye model at all temperatures. The more elementary formulae given further down give the asymptotic behavior in the limit of low and high temperatures. Debye's derivationActually, Debye derived his equation somewhat differently and more simply. Using the solid mechanics of a continuous medium, he found that the number of vibrational states with a frequency less than a particular value was asymptotic to in which V is the volume and F is a factor which he calculated from elasticity coefficients and density. Combining this with the expected energy of a harmonic oscillator at temperature T (already used by Einstein in his model) would give an energy of if the vibrational frequencies continued to infinity. This form gives the T4 behavior which is correct at low temperatures. But Debye realized that there could not be more than 3N vibrational states for N atoms. He made the assumption that in an atomic solid, the spectrum of frequencies of the vibrational states would continue to follow the above rule, up to a maximum frequency νm chosen so that the total number of states is 3N: Debye knew that this assumption was not really correct (the higher frequencies are more closely spaced than assumed), but it guarantees the proper behavior at high temperature (the Dulong-Petit law). The energy is then given by:
where D3 is the function later given the name of third-order Debye function. Low temperature limitThe temperature of a Debye solid is said to be low if This definite integral can be evaluated exactly: In the low temperature limit, the limitations of the Debye model mentioned above do not apply, and it gives a correct relationship between (phononic) heat capacity, temperature, the elastic coefficients, and the volume per atom (the latter quantities being contained in the Debye temperature). High temperature limitThe temperature of a Debye solid is said to be high if T > > TD. This is the Dulong-Petit law, and is fairly accurate although it does not take into account anharmonicity, which causes the heat capacity to rise further. The total heat capacity of the solid, if it is a conductor or semiconductor, may also contain a non-negligible contribution from the electrons. Debye versus Einstein
So how closely do the Debye and Einstein models correspond to experiment? -- Surprisingly close, but Debye is correct at low temperatures whereas Einstein is not. How different are the models? To answer that question one would naturally plot the two on the same set of axes... except one can't. Both the Einstein model and the Debye model provide a functional form for the heat capacity. They are models, and no model is without a scale. A scale relates the model to its real-world counterpart. One can see that the scale of the Einstein model, which is given by is ε / k. And the scale of the Debye model is TD, the Debye temperature. Both are usually found by fitting the models to the experimental data. (The Debye temperature can theoretically be calculated from the speed of sound and crystal dimensions.) Because the two methods approach the problem from different directions and different geometries, Einstein and Debye scales are not the same, that is to say which means that plotting them on the same set of axes makes no sense. They are two models of the same thing, but of different scales. If one defines Einstein temperature as then one can say and, to relate the two, we must seek the ratio The Einstein solid is composed of single-frequency quantum harmonic oscillators, which makes the Einstein temperature and the sought ratio is therefore Now both models can be plotted on the same graph. Note that this ratio is the cube root of the ratio of the volume of one octant of a 3-dimensional sphere to the volume of the cube that contains it, which is just the correction factor used by Debye when approximating the energy integral above. Debye temperature tableEven though the Debye model is not completely correct, it gives a good approximation for the low temperature heat capacity of insulating, crystalline solids where other contributions (such as highly mobile conduction electrons) are negligible. For metals, the electron contribution to the heat is proportional to T, which at low temperatures dominates the Debye T3 result for lattice vibrations. In this case, the Debye model can only be said to approximate the lattice contribution to the specific heat. The following table lists Debye temperatures for several substances:
See alsoReferences
Categories: Condensed matter physics | Thermodynamics |
||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Debye_model". A list of authors is available in Wikipedia. |





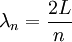
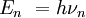
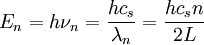
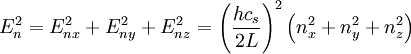
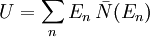
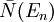 is the number of phonons in the box with energy
is the number of phonons in the box with energy 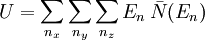
![\sqrt[3]{N}](images/math/0/0/1/00166fc2a768c979bb73b7291855c0ba.png) atoms per side. Atom separation is then given by
atoms per side. Atom separation is then given by ![L/\sqrt[3]{N}](images/math/c/3/e/c3e4bc982ebd4a4f3a79a823ea7657eb.png) , and the minimum wavelength is
, and the minimum wavelength is
![\lambda_{\rm min} = {2L \over \sqrt[3]{N}}](images/math/2/3/4/234e4c895166c89df126ae21f69a68db.png)
![n_{\rm max} = \sqrt[3]{N}](images/math/2/b/9/2b9f374aaf71f3e9823e9738e7b94833.png)
![U = \sum_{n_x}^{\sqrt[3]{N}}\sum_{n_y}^{\sqrt[3]{N}}\sum_{n_z}^{\sqrt[3]{N}}E_n\,\bar{N}(E_n)](images/math/3/9/e/39e9de46b44b97546a14f6ee390dec1b.png)
![U \approx\int_0^{\sqrt[3]{N}}\int_0^{\sqrt[3]{N}}\int_0^{\sqrt[3]{N}} E(n)\,\bar{N}\left(E(n)\right)\,dn_x\, dn_y\, dn_z](images/math/7/b/0/7b0f1671841079db6fcb7400f0104f45.png)
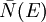 , the number of phonons with energy
, the number of phonons with energy 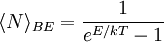
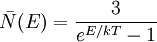
![U = \int_0^{\sqrt[3]{N}}\int_0^{\sqrt[3]{N}}\int_0^{\sqrt[3]{N}} E(n)\,{3\over e^{E(n)/kT}-1}\,dn_x\, dn_y\, dn_z](images/math/e/2/b/e2bbd92a96004c2c96b4583e71fca84c.png)
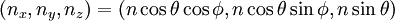
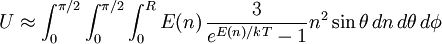
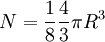
![R = \sqrt[3]{6N\over\pi}](images/math/8/2/5/825e65ae4b9bdbeaacf00b312a9457f9.png)
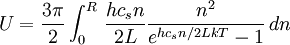
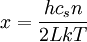 ,
,
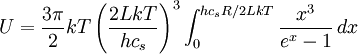
![T_D\ \stackrel{\mathrm{def}}{=}\ {hc_sR\over2Lk} = {hc_s\over2Lk}\sqrt[3]{6N\over\pi} = {hc_s\over2k}\sqrt[3]{{6\over\pi}{N\over V}}](images/math/4/e/8/4e827a6c66a38402d9b87456c656b671.png)
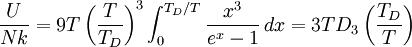
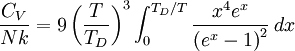
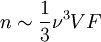
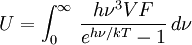
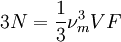
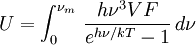
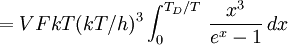
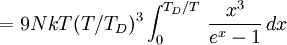
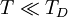 , leading to
, leading to
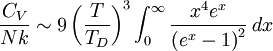
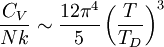
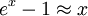 if
if 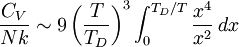
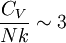
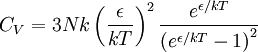
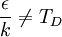
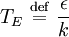
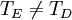
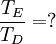
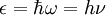 . That frequency, if it indeed existed, would be related to the speed of sound in the solid... even though there is no sound in Einstein solid. If one imagines the propagation of sound as a sequence of atoms hitting one another, then it becomes obvious that the frequency of oscillation must correspond to the minimum wavelength sustainable by the atomic lattice,
. That frequency, if it indeed existed, would be related to the speed of sound in the solid... even though there is no sound in Einstein solid. If one imagines the propagation of sound as a sequence of atoms hitting one another, then it becomes obvious that the frequency of oscillation must correspond to the minimum wavelength sustainable by the atomic lattice, ![\nu = {c_s\over\lambda} = {c_s\sqrt[3]{N}\over 2L} = {c_s\over 2}\sqrt[3]{N\over V}](images/math/1/6/6/166f21b7ee0f757bb0aa0e4d25e9735b.png)
![T_E = {\epsilon\over k} = {h\nu\over k} = {h c_s\over 2k}\sqrt[3]{N\over V}](images/math/b/9/3/b93a0098ed3f4ad33b2d60e138996542.png)
![{T_E\over T_D} = \sqrt[3]{\pi\over6}](images/math/d/7/4/d747dfae3485d6c340b8a71848b40438.png)


