To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Phonon
In physics, a phonon is a quantized mode of vibration occurring in a rigid crystal lattice, such as the atomic lattice of a solid.[1] The study of phonons is an important part of solid state physics, because phonons play a major role in many of the physical properties of solids, including a material's thermal and electrical conductivities. In particular, the properties of long-wavelength phonons give rise to sound in solids -- hence the name phonon from the Greek φονή (phonē) = voice.[2] In insulating solids, phonons are also the primary mechanism by which heat conduction takes place. Phonons are a quantum mechanical version of a special type of vibrational motion, known as normal modes in classical mechanics, in which each part of a lattice oscillates with the same frequency. These normal modes are important because, according to a well-known result in classical mechanics, any arbitrary vibrational motion of a lattice can be considered as a superposition of normal modes with various frequencies; in this sense, the normal modes are the elementary vibrations of the lattice. Although normal modes are wave-like phenomena in classical mechanics, they acquire certain particle-like properties when the lattice is analysed using quantum mechanics (see wave-particle duality.) They are then known as phonons. Product highlight
Repeating derivation of normal modesThe equations in this subsection either do not use axioms of quantum mechanics or use relations for which there exists a direct correspondence in classical mechanics. Mechanics of particles on a latticeConsider a rigid regular (or "crystalline") lattice composed of N particles. (We will refer to these particles as "atoms", though in a real solid they may actually be ions.) N is some large number, say around 1023 (on the order of Avogadro's number) for a typical piece of solid. If the lattice is rigid, the atoms must be exerting forces on one another, so as to keep each atom near its equilibrium position. In real solids, these forces include Van der Waals forces, covalent bonds, and so forth, all of which are ultimately due to the electric force; magnetic and gravitational forces are generally negligible. The forces between each pair of atoms may be characterized by some potential energy function V, depending on the separation of the atoms. The potential energy of the entire lattice is the sum of all the pairwise potential energies:
where It is extremely difficult to solve this many-body problem in full generality, in either classical or quantum mechanics. In order to simplify the task, we introduce two important approximations. Firstly, we only perform the sum over neighbouring atoms. Although the electric forces in real solids extend to infinity, this approximation is nevertheless valid because the fields produced by distant atoms are screened. Secondly, we treat the potentials The resulting lattice may be visualized as a system of balls connected by springs. The following figure shows a cubic lattice, which is a good model for many types of crystalline solid. Other lattices include a linear chain, which is a very simple lattice which we will shortly use for modelling phonons. Other common lattices may be found in the article on crystal structure.
The potential energy of the lattice may now be written as
Here, Lattice wavesDue to the connections between atoms, the displacement of one or more atoms from their equilibrium positions will give rise to a set of vibration waves propagating through the lattice. One such wave is shown in the figure below. The amplitude of the wave is given by the displacements of the atoms from their equilibrium positions. The wavelength There is a minimum possible wavelength, given by the equilibrium separation a between atoms. As we shall see in the following sections, any wavelength shorter than this can be mapped onto a wavelength longer than a, due to effects similar to that in aliasing. Not every possible lattice vibration has a well-defined wavelength and frequency. However, the normal modes (which, as we mentioned in the introduction, are the elementary building-blocks of lattice vibrations) do possess well-defined wavelengths and frequencies. We will now examine it in detail. Phonon dispersion of a one-dimensional chain of identical atomsConsider a one-dimensional quantum mechanical harmonic chain of N identical atoms. This is the simplest quantum mechanical model of a lattice, and we will see how phonons arise from it. The formalism that we will develop for this model is readily generalizable to two and three dimensions. The Hamiltonian for this system is
where We introduce a set of
The quantity
The upper bound to By inverting the discrete Fourier transforms to express the
In other words, the normal coordinates and their conjugate momenta obey the same commutation relations as position and momentum operators! Writing the Hamiltonian in terms of these quantities,
where
Notice that the couplings between the position variables have been transformed away; if the Three-dimensional phononsIt is straightforward, though tedious, to generalize the above to a three-dimensional lattice. One finds that the wave number k is replaced by a three-dimensional wave vector k. Furthermore, each k is now associated with three normal coordinates. The new indices s = 1, 2, 3 label the polarization of the phonons. In the one dimensional model, the atoms were restricted to moving along the line, so all the phonons corresponded to longitudinal waves. In three dimensions, vibration is not restricted to the direction of propagation, and can also occur in the perpendicular plane, like transverse waves. This gives rise to the additional normal coordinates, which, as the form of the Hamiltonian indicates, we may view as independent species of phonons. Dispersion relationIn the above discussion, we have obtained an equation that relates the frequency of a phonon,
This is known as a dispersion relation. The speed of propagation of a phonon, which is also the speed of sound in the lattice, is given by the slope of the dispersion relation, For a crystal that has at least two atoms in a unit cell (which may or may not be different), the dispersion relations exhibit two types of phonons, namely, optical and acoustic modes corresponding to the upper and lower sets of curves in the diagram, respectively. The vertical axis is the energy or frequency of phonon, while the horizontal axis is the wave-vector. The boundaries at -km and km are those of the first Brillouin zone. The blue, violet, and brown curves are those of longitudinal acoustic, transverse acoustic 1, and transverse acoutic 2 modes, respectively. In some crystals the two transverse acoustic modes have exactly the same dispersion curve. It is also interesting that for a crystal with N ( > 2) different atoms in a primitive cell, there are always three acoustic modes. The number of optical modes is 3N - 3. Many phonon dispersion curves have been measured by neutron scattering. The physics of sound in fluids differs from the physics of sound in solids, although both are density waves: sound waves in fluids only have longitudinal components, whereas sound waves in solids have longitudinal and transverse components. This is because fluids can't support shear stresses. (but see viscoelastic fluids, which only apply to high frequencies, though). Acoustic and optical phononsIn solids with more than one atom in the smallest unit cell, there are two types of phonons: "acoustic" phonons and "optical" phonons. "Acoustic phonons", which are the phonons described above, have frequencies that become small at the long wavelengths, and correspond to sound waves in the lattice. Longitudinal and transverse acoustic phonons are often abbreviated as LA and TA phonons, respectively. "Optical phonons," which arise in crystals that have more than one atom in the smallest unit cell, always have some minimum frequency of vibration, even when their wavelength is large. They are called "optical" because in ionic crystals (like sodium chloride) they are excited very easily by light (in fact, infrared radiation). This is because they correspond to a mode of vibration where positive and negative ions at adjacent lattice sites swing against each other, creating a time-varying electrical dipole moment. Optical phonons that interact in this way with light are called infrared active. Optical phonons which are Raman active can also interact indirectly with light, through Raman scattering. Optical phonons are often abbreviated as LO and TO phonons, for the longitudinal and transverse varieties respectively. PhononsIn fact, the above derived Hamiltonian looks like the classical Hamilton function, but if its interpreted as an operator it describes a quantum field theory of non-interacting bosons. This leads to new physics. The energy spectrum of this Hamiltonian is easily obtained by the method of ladder operators, similar to the quantum harmonic oscillator problem. We introduce a set of ladder operators defined by
The ladder operators satisfy the following identities:
As with the quantum harmonic oscillator, we can then show that We can immediately deduce two important properties of phonons. Firstly, phonons are bosons, since any number of identical excitations can be created by repeated application of the creation operator It is not a priori obvious that these excitations generated by the
One can show that, for any two atoms
which is exactly what we would expect for a lattice wave with frequency In three dimensions the Hamiltonian has the form
Crystal momentum
It is tempting to treat a phonon with wave vector
where
for any integer It is usually convenient to consider phonon wave vectors It is interesting that similar consideration is needed in analog-to-digital conversion where aliasing may occur under certain conditions.
Thermodynamic propertiesA crystal lattice at zero temperature lies in its ground state, and contains no phonons. According to thermodynamics, when the lattice is held at a non-zero temperature its energy is not constant, but fluctuates randomly about some mean value. These energy fluctuations are caused by random lattice vibrations, which can be viewed as a gas of phonons. (Note: the random motion of the atoms in the lattice is what we usually think of as heat.) Because these phonons are generated by the temperature of the lattice, they are sometimes referred to as thermal phonons. Unlike the atoms which make up an ordinary gas, thermal phonons can be created or destroyed by random energy fluctuations. In the language of statistical mechanics this means that the chemical potential for adding a phonon is zero. It is very important to note that this behaviour takes us away from the harmonic potential mentioned earlier, and into the anharmonic regime. The behaviour of thermal phonons is similar to the photon gas produced by an electromagnetic cavity, wherein photons may be emitted or absorbed by the cavity walls. This similarity is not coincidental, for it turns out that the electromagnetic field behaves like a set of harmonic oscillators; see Black-body radiation. Both gases obey the Bose-Einstein statistics: in thermal equilibrium and within the harmonic regime, the probability of finding phonons (or photons) in a given state with a given angular frequency is:
where See also
References
Categories: Condensed matter physics | Bosons |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Phonon". A list of authors is available in Wikipedia. |





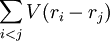
 is the position of the
is the position of the  th atom, and
th atom, and  is the potential energy between two atoms.
is the potential energy between two atoms.
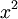 .)
.)
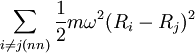
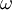 is the natural frequency of the harmonic potentials, which we assume to be the same since the lattice is regular.
is the natural frequency of the harmonic potentials, which we assume to be the same since the lattice is regular. 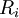 is the position coordinate of the
is the position coordinate of the 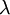 is marked.
is marked.
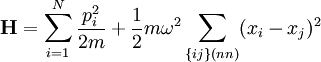
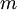 is the mass of each atom, and
is the mass of each atom, and 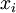 and
and 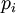 are the position and
are the position and 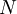 "normal coordinates"
"normal coordinates" 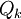 , defined as the discrete Fourier transforms of the
, defined as the discrete Fourier transforms of the 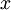 's and
's and 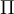 defined as the Fourier transforms of the
defined as the Fourier transforms of the 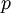 's:
's:
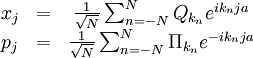
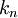 will turn out to be the wave number of the phonon, i.e.
will turn out to be the wave number of the phonon, i.e. 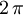 divided by the wavelength. It takes on quantized values, because the number of atoms is finite. The form of the quantization depends on the choice of boundary conditions; for simplicity, we impose periodic boundary conditions, defining the
divided by the wavelength. It takes on quantized values, because the number of atoms is finite. The form of the quantization depends on the choice of boundary conditions; for simplicity, we impose periodic boundary conditions, defining the 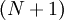 th atom as equivalent to the first atom. Physically, this corresponds to joining the chain at its ends. The resulting quantization is
th atom as equivalent to the first atom. Physically, this corresponds to joining the chain at its ends. The resulting quantization is
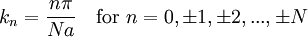
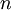 comes from the minimum wavelength imposed by the lattice spacing
comes from the minimum wavelength imposed by the lattice spacing 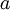 , as discussed above.
, as discussed above.
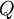 's in terms of the
's in terms of the ![\left[ Q_k , \Pi_{k'} \right] = i \hbar \delta_{k k'} \quad ;\quad \left[ Q_k , Q_{k'} \right] = \left[ \Pi_k , \Pi_{k'} \right] = 0](images/math/c/d/e/cdecfe4f3b66be4df3495326ad4d62a2.png)
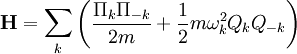
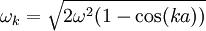
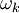 , to its wave number
, to its wave number 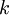 :
:
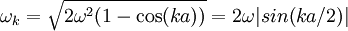
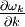 (see group velocity.) At low values of
(see group velocity.) At low values of 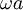 , independent of the phonon frequency. As a result, packets of phonons with different (but long) wavelengths can propagate for large distances across the lattice without breaking apart. This is the reason that sound propagates through solids without significant distortion. This behavior fails at large values of
, independent of the phonon frequency. As a result, packets of phonons with different (but long) wavelengths can propagate for large distances across the lattice without breaking apart. This is the reason that sound propagates through solids without significant distortion. This behavior fails at large values of 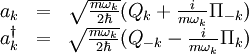
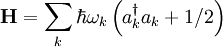
![[a_k , a_{k'}^{\dagger} ] = \delta_{kk'}](images/math/c/5/0/c5052c89ba2167155b7bfe568f8f37d1.png)
![[a_k , a_{k'} ] = [a_k^{\dagger} , a_{k'}^{\dagger} ] = 0.](images/math/5/4/6/54686099e03a6e896a4ac9e9843ca83c.png)
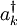 and
and 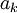 respectively create and destroy one excitation of energy
respectively create and destroy one excitation of energy 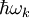 . These excitations are phonons.
. These excitations are phonons.
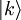 denote a state with a single quantum of mode
denote a state with a single quantum of mode 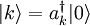
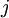 and
and 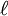 ,
,
![\langle k | x_j(t) x_{\ell}(0) | k \rangle = \frac{\hbar}{Nm\omega_k} \cos \left[ k(j-\ell)a - \omega_k t \right] + \langle 0 | x_j(t) x_\ell(0) |0 \rangle](images/math/e/e/c/eec49f5a9b9a4a9c7f4d9d4f9f6ea73b.png)
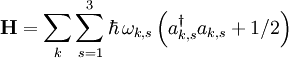
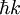 , by analogy to
, by analogy to 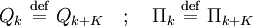
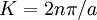
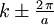 ,
, 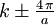 , and so forth. Physically, the reciprocal lattice vectors act as additional "chunks" of momentum which the lattice can impart to the phonon.
, and so forth. Physically, the reciprocal lattice vectors act as additional "chunks" of momentum which the lattice can impart to the phonon. 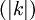 in their "family". The set of all such wave vectors defines the first
in their "family". The set of all such wave vectors defines the first 
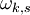 is the frequency of the phonons (or photons) in the state,
is the frequency of the phonons (or photons) in the state,  is
is 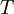 is the temperature.
is the temperature.


