To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Reciprocal latticeIn crystallography, the reciprocal lattice of a Bravais lattice is the set of all vectors K such that for all lattice point position vectors R. The reciprocal lattice is itself a Bravais lattice, and the reciprocal of the reciprocal lattice is the original lattice. For a three dimensional lattice, defined by its primitive vectors Using column vector representation of (reciprocal) primitive vectors, the formula above can be rewritten using matrix inversion: This method appeals to the definition, and allows generalization to arbitrary dimensions. Curiously, the cross product formula dominates introductory materials on crystallography. The above definition is called the "physics" definition, as the factor of 2π comes naturally from the study of periodic structures. An equivalent definition, the "crystallographer's" definition, comes from defining the reciprocal lattice to be and so on for the other vectors. The crystallographer's definition has the advantage that the definition of Each point (hkl) in the reciprocal lattice corresponds to a set of lattice planes (hkl) in the real space lattice. The direction of the reciprocal lattice vector corresponds to the normal to the real space planes, and the magnitude of the reciprocal lattice vector is equal to the reciprocal of the interplanar spacing of the real space planes. The reciprocal lattice plays a fundamental role in most analytic studies of periodic structures, particularly in the theory of diffraction. For Bragg reflections in neutron and X-ray diffraction, the momentum difference between incoming and diffracted X-rays of a crystal is a reciprocal lattice vector. The diffraction pattern of a crystal can be used to determine the reciprocal vectors of the lattice. Using this process, one can infer the atomic arrangement of a crystal. The Brillouin zone is a primitive unit cell of the reciprocal lattice. Product highlight
Reciprocal lattices of various crystalsReciprocal lattices for the cubic crystal system are as follows. Simple cubic latticeWe find that the simple cubic Bravais lattice, with cubic primitive cell of side a, has for its reciprocal a simple cubic lattice with a cubic primitive cell of side Face-centered cubic latticeThe reciprocal lattice to an FCC lattice is the BCC lattice. Finding the reciprocal lattice of a face-centered cubicConsider an FCC compound unit cell. Locate a primitive unit cell of the FCC--i.e., a unit cell with one lattice point. Now take one of the vertices of the primitive unit cell as the origin. Give the basis vectors of the real lattice. Then from the known formulae you can calculate the basis vectors of the reciprocal lattice. These reciprocal lattice vectors of the FCC represent the basis vectors of a BCC real lattice. Note that the basis vectors of a real BCC lattice and the reciprocal lattice of an FCC resemble each other in direction but not in magnitude. Body-centered cubic latticeThe reciprocal lattice to a BCC lattice is the FCC lattice. It can be easily proven that only the Bravais lattices which have 90 degrees between Mathematics of the dual latticeThere are actually two versions in mathematics of the abstract dual lattice concept, for a given lattice L in a real vector space V, of finite dimension. The first, which generalises directly the reciprocal lattice construction, uses Fourier analysis. It may be stated simply in terms of Pontryagin duality. The dual group V^ to V is again a real vector space, and its closed subgroup L^ dual to L turns out to be a lattice in V^. Therefore L^ is the natural candidate for dual lattice, in a different vector space (of the same dimension). The other aspect is seen in the presence of a quadratic form Q on V; if it is non-degenerate it allows an identification of the dual space V* of V with V. The relation of V* to V is not intrinsic; it depends on a choice of Haar measure (volume element) on V. But given an identification of the two, which is in any case well-defined up to a scalar, the presence of Q allows one to speak to the dual lattice to L while staying within V. Categories: Crystallography | Neutron related techniques | Diffraction |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Reciprocal_lattice". A list of authors is available in Wikipedia. |


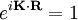
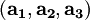 , its reciprocal lattice can be determined by generating its three reciprocal primitive vectors, through the formula,
, its reciprocal lattice can be determined by generating its three reciprocal primitive vectors, through the formula,
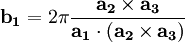
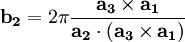
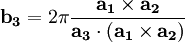
![\left[\mathbf{b_{1}}\mathbf{b_{2}}\mathbf{b_{3}}\right]^T = 2\pi\left[\mathbf{a_{1}}\mathbf{a_{2}}\mathbf{a_{3}}\right]^{-1}](images/math/4/c/5/4c5c805f61c4862995e56a7c7c1387ed.png)
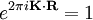 which changes the definitions of the reciprocal lattice vectors to be
which changes the definitions of the reciprocal lattice vectors to be
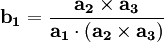
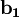 is just the reciprocal magnitude of
is just the reciprocal magnitude of 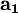 in the direction of
in the direction of 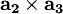 , dropping the factor of
, dropping the factor of 


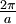 (
(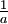 in the crystallographer's definition). The cubic lattice is therefore said to be dual, having its reciprocal lattice being identical (up to a numerical factor).
in the crystallographer's definition). The cubic lattice is therefore said to be dual, having its reciprocal lattice being identical (up to a numerical factor).
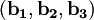 parallel to their real-space vectors.
parallel to their real-space vectors.


