To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Normal modeA normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building or bridge, has a set of normal modes (and frequencies) that depend on its structure and composition. It is common to use a spring-mass system to illustrate a deformable structure. When such a system is excited at one of these natural frequencies, all of the masses move at the same frequency. The phases of the masses are either exactly the same or exactly opposite. The practical significance of this can be illustrated by a mass-spring model of a building. If an earthquake excites the system near one of the natural frequencies, the displacement of one floor with respect to another will be maximum. Obviously, buildings can only withstand this displacement up to a certain point. Being able to model a building and find its normal modes is an easy way to check the safety of a building's design. The concept of normal modes also finds application in wave theory, optics and quantum mechanics. Product highlight
Example - normal modes of coupled oscillatorsConsider two bodies (not affected by gravity), each of mass M, attached to three springs, each with spring constant K. They are attached in the following manner: where the edge points are fixed and cannot move. We'll use x1(t) to denote the displacement of the leftmost mass, and x2(t) to denote the displacement of the rightmost. If we denote the second derivative of x(t) with respect to time as x″, the equations of motion are: Since we expect oscillatory motion, we try: Substituting these into the equations of motion gives us: Since the exponential factor is common to all terms, we omit it and simplify: And in matrix representation: For this equation to have a non-trivial solution, the matrix on the left must be singular, therefore the determinant of the matrix must be equal to 0, so: Solving for ω, we have two solutions:
If we substitute ω1 into the matrix and solve for (A1,A2), we get (1, 1). If we substitute ω2, we get (1, -1). (These vectors are eigenvectors, and the frequencies are eigenvalues.) The first normal mode is: and the second normal mode is: The general solution is a superposition of the normal modes where c1, c2, φ1, and φ2, are determined by the initial conditions of the problem. The process demonstrated here can be generalized and formulated using the formalism of Lagrangian mechanics or Hamiltonian mechanics. Standing wavesA standing wave is a continuous form of normal mode. In a standing wave, all the space elements (i.e (x,y,z) coordinates) are oscillating in the same frequency and in phase (reaching the equilibrium point together), but each has a different amplitude.
The general form of a standing wave is:
where f(x, y, z) represents the dependence of amplitude on location and the cosine\sine are the oscillations in time. Physically, standing waves are formed by the interference (superposition) of waves and their reflections (although one may also say the opposite; that a moving wave is a superposition of standing waves). The geometric shape of the medium determines what would be the interference pattern, thus determines the f(x, y, z) form of the standing wave. This space-dependence is called a normal mode. Usually, for problems with continuous dependence on (x,y,z) there is no single or finite number of normal modes, but there are infinitely many normal modes. If the problem is bounded (i.e it is defined on a finite section of space) there are countably many (a discrete infinity of ) normal modes (usually numbered n = 1,2,3,...). If the problem is not bounded, there is a continuous spectrum of normal modes. The allowed frequencies are dependent on the normal modes, as well as on physical constants of the problem (density, tension, pressure, etc.) which set the phase velocity of the wave. The range of all possible normal frequencies is called the frequency spectrum. Usually, each frequency is modulated by the amplitude at which it has arisen, creating a graph of the power spectrum of the oscillations. When relating to music, normal modes of vibrating instruments (strings, air pipes, drums, etc.) are called "harmonics". Normal modes in quantum mechanicsIn quantum mechanics, a state is the probability density to measure the particle in place x at time t. Usually, when involving some sort of potential, the wavefunction is decomposed into a superposition of energy eigenstates, each oscillating with frequency of The eigenstates have a physical meaning further than an orthonormal basis. When the energy of the system is measured, the wavefunction collapses into one of its eigenstates and so the particle wavefunction is described by the pure eigenstate corresponding to the measured energy. See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Normal_mode". A list of authors is available in Wikipedia. |
- Beta_blocker
- Table_of_nuclides
- Heat_engine
- The use of MRI to directly observe metal-ion dissolution in lithium battery cathodes - There is enormous promise in how this technique can increase the ability to understand how reactions within these batteries work and how to test alternate battery technology
- Kelvin





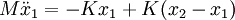
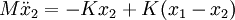
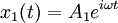
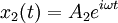
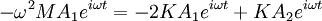
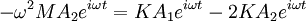
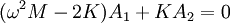
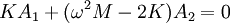
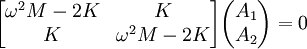
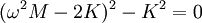
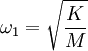 ,
,
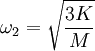 ,
,
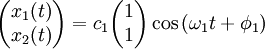
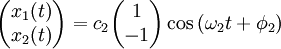
 of a system is described by a wavefunction
of a system is described by a wavefunction 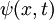 which solves the Schrödinger equation. The square of the absolute value of
which solves the Schrödinger equation. The square of the absolute value of 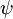 ,i.e.
,i.e.
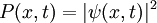
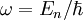 . Thus, we may write
. Thus, we may write