To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Virial coefficientVirial coefficients Bi appear as coefficients in the virial expansion of the pressure of a many-particle system in powers of the density. They are characteristic of the interaction potential between the particles and in general depend on the temperature. The second virial coefficient B2 depends only on the pair interaction between the particles, the third (B3) depends on 2- and non-additive 3-body interactions, and so on. Product highlightThe first step in obtaining a closed expression for virial coefficients is a cluster expansion[1] of the grand canonical partition function
Here p is the pressure, V is the volume of the vessel containing the particles, kB is Boltzmann's constant, T is the absolute temperature, λ = exp[μ / (kBT)], with μ the chemical potential. The quantity Qn is the canonical partition function of a subsystem of n particles: Here
These are quantum-statistical expressions containing kinetic energies. Note that the one-particle partition function Q1 contains only a kinetic energy term. In the classical limit
The derivation of higher than B3 virial coefficients becomes quickly a complex combinatorial problem. Making the classical approximation and neglecting non-additive interactions (if present), the combinatorics can be handled graphically as first shown by Joseph E. Mayer and Maria Goeppert-Mayer [2]. They introduced the function and wrote the cluster expansion in terms of these functions. Here
Definition in terms of graphsThe virial coeffcients Bi are related to the irreducible Mayer cluster integrals βi through
The rule for turning these graphs into integrals is as follows:
The first two cluster integrals are
In particular we get where particle 2 was assumed to define the origin ( See alsoBoyle temperature - temperature at which the second virial coefficient B2 vanishes Literature
See further:
|
||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Virial_coefficient". A list of authors is available in Wikipedia. |





![Q_n = \operatorname{tr} [ e^{- H(1,2,\ldots,n)/(k_B T)} ].](images/math/3/0/8/308e91e654ba997b097dc7a20c78b62b.png)
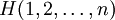 is the Hamiltonian (energy operator) of a subsystem of
is the Hamiltonian (energy operator) of a subsystem of
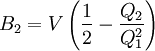
![B_3 = V^2 \left[ \frac{2Q_2}{Q_1^2}\Big( \frac{2Q_2}{Q_1^2}-1\Big) -\frac{1}{3}\Big(\frac{6Q_3}{Q_1^3}-1\Big) \right]](images/math/5/2/6/52674b1264feba3cd81eb6ac97b12c47.png) .
.
 the kinetic energy operators commute with the potential operators and
the kinetic energies in numerator and denominator cancel mutually. The trace (tr) becomes an integral over the configuration space. It follows that classical virial coefficients depend on the interactions between the particles only and are given as integrals over the particle coordinates.
the kinetic energy operators commute with the potential operators and
the kinetic energies in numerator and denominator cancel mutually. The trace (tr) becomes an integral over the configuration space. It follows that classical virial coefficients depend on the interactions between the particles only and are given as integrals over the particle coordinates.
![f(1,2) = \exp\left[- \frac{u(|\vec{r}_1- \vec{r}_2|)}{k_B T}\right] - 1](images/math/2/d/b/2db591a77a7c08cef9fe617dc505b9c4.png)
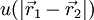 is the interaction between particle 1 and 2 (which are assumed to be identical particles).
is the interaction between particle 1 and 2 (which are assumed to be identical particles).
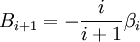
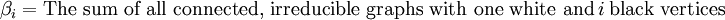
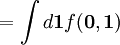
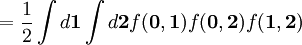
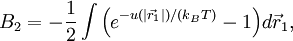
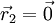 ).
This classical expression for the second virial coefficient was first derived by L. S.
Ornstein in his 1908 Leiden University Ph.D. thesis.
).
This classical expression for the second virial coefficient was first derived by L. S.
Ornstein in his 1908 Leiden University Ph.D. thesis.


