To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Partition function (statistical mechanics)In statistical mechanics, the partition function Z is an important quantity that encodes the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas. Most of the thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. There are actually several different types of partition functions, each corresponding to different types of statistical ensemble (or, equivalently, different types of free energy.) The canonical partition function applies to a canonical ensemble, in which the system is allowed to exchange heat with the environment at fixed temperature, volume, and number of particles. The grand canonical partition function applies to a grand canonical ensemble, in which the system can exchange both heat and particles with the environment, at fixed temperature, volume, and chemical potential. Other types of partition functions can be defined for different circumstances. Product highlight
Canonical partition functionDefinitionSuppose we have a thermodynamically large system that is in constant thermal contact with the environment, which has temperature T, with both the volume of the system and the number of constituent particles fixed. This kind of system is called a canonical ensemble. Let us label the exact states (microstates) that the system can occupy by j (j = 1, 2, 3, ...), and denote the total energy of the system when it is in microstate j as Ej. Generally, these microstates can be regarded as discrete quantum states of the system. The canonical partition function is where the "inverse temperature" β is conventionally defined as with kB denoting Boltzmann's constant. Sometimes degeneracy of states is also used and the partition function becomes
where gj is the degeneracy factor. In classical statistical mechanics, it is not really correct to express the partition function as a sum of discrete terms, as we have done. In classical mechanics, the position and momentum variables of a particle can vary continuously, so the set of microstates is actually uncountable. In this case, some form of coarse graining procedure must be carried out, which essentially amounts to treating two mechanical states as the same microstate if the differences in their position and momentum variables are "not too large". The partition function then takes the form of an integral. For instance, the partition function of a gas of N classical particles is
where h is some infinitesimal quantity with units of action (usually taken to be Planck's constant, in order to be consistent with quantum mechanics), and H is the classical Hamiltonian. The reason for the N! factor is discussed below. For simplicity, we will use the discrete form of the partition function in this article, but our results will apply equally well to the continuous form.
For more details on the derivation of the above classical partition function, see
Configuration integral (statistical mechanics), where
the partition function is denoted by
In quantum mechanics, the partition function can be more formally written as a trace over the state space (which is independent of the choice of basis): where H is the quantum Hamiltonian operator. The exponential of an operator can be defined, for purely physical considerations, using the exponential power series. Meaning and significanceIt may not be obvious why the partition function, as we have defined it above, is an important quantity. Firstly, let us consider what goes into it. The partition function is a function of the temperature T and the microstate energies E1, E2, E3, etc. The microstate energies are determined by other thermodynamic variables, such as the number of particles and the volume, as well as microscopic quantities like the mass of the constituent particles. This dependence on microscopic variables is the central point of statistical mechanics. With a model of the microscopic constituents of a system, one can calculate the microstate energies, and thus the partition function, which will then allow us to calculate all the other thermodynamic properties of the system. The partition function can be related to thermodynamic properties because it has a very important statistical meaning. The probability Pj that the system occupies microstate j is This is the well-known Boltzmann factor. (For a detailed derivation of this result, see canonical ensemble.) The partition function thus plays the role of a normalizing constant (note that it does not depend on j), ensuring that the probabilities add up to one: This is the reason for calling Z the "partition function": it encodes how the probabilities are partitioned among the different microstates, based on their individual energies. The letter Z stands for the German word Zustandssumme, "sum over states". Calculating the thermodynamic total energyIn order to demonstrate the usefulness of the partition function, let us calculate the thermodynamic value of the total energy. This is simply the expected value, or ensemble average for the energy, which is the sum of the microstate energies weighted by their probabilities: or, equivalently, Incidentally, one should note that if the microstate energies depend on a parameter λ in the manner then the expected value of A is This provides us with a trick for calculating the expected values of many microscopic quantities. We add the quantity artificially to the microstate energies (or, in the language of quantum mechanics, to the Hamiltonian), calculate the new partition function and expected value, and then set λ to zero in the final expression. This is analogous to the source field method used in the path integral formulation of quantum field theory. Relation to thermodynamic variablesIn this section, we will state the relationships between the partition function and the various thermodynamic parameters of the system. These results can be derived using the method of the previous section and the various thermodynamic relations. As we have already seen, the thermodynamic energy is The variance in the energy (or "energy fluctuation") is The heat capacity is The entropy is where A is the Helmholtz free energy defined as A = U - TS, where U= Partition functions of subsystemsSuppose a system is subdivided into N sub-systems with negligible interaction energy. If the partition functions of the sub-systems are ζ1, ζ2, ..., ζN, then the partition function of the entire system is the product of the individual partition functions: If the sub-systems have the same physical properties, then their partition functions are equal, ζ1 = ζ2 = ... = ζ, in which case
However, there is a well-known exception to this rule. If the sub-systems are actually identical particles, in the quantum mechanical sense that they are impossible to distinguish even in principle, the total partition function must be divided by a N! (N factorial): This is to ensure that we do not "over-count" the number of microstates. While this may seem like a strange requirement, it is actually necessary to preserve the existence of a thermodynamic limit for such systems. This is known as the Gibbs paradox. ExamplesA specific example of the partition function, expressed in terms of the mathematical formalism of measure theory, is presented in the article on the Potts model. Grand canonical partition functionDefinitionIn a manner similar to the definition of the canonical partition function for the canonical ensemble, we can define a grand canonical partition function for a grand canonical ensemble, a system that can exchange both heat and particles with the environment, which has a constant temperature T, volume V, and chemical potential μ. The grand canonical partition function, although conceptually more involved, simplifies the
calculation of the physics of quantum systems. The grand canonical partition function where N is the total number of particles in the volume V, and index i runs over every microstate of the system, with ni being the number of particles in state i and εi being the energy of state i. {ni} is the set of all possible occupation numbers for each of the microstates such that Σini = N. For example, consider the N = 3 term in the above sum. One possible set of occupation numbers would be {ni} = 0,1,0,2,0... and the contribution of this set of occupation numbers to the N = 3 term would be For bosons, the occupation numbers can take any integer values as long as their sum is equal to N. For fermions, the Pauli exclusion principle requires that the occupation numbers only be 0 or 1, again adding up to N. Specific expressionsThe above expression for the grand partition function can be shown to be mathematically equivalent to: (Note: the above product is sometimes taken over all states with equal energy, rather than over each state, in which case the individual partition functions must be raised to a power gi where gi is the number of such states. gi is also referred to as the "degeneracy" of states.) For a system composed of bosons: and for a system composed of fermions: For the case of a Maxwell-Boltzmann gas, we must use "correct Boltzmann counting" and divide the Boltzmann factor Relation to thermodynamic variablesJust as with the canonical partition function, the grand canonical partition function can be used to calculate thermodynamic and statistical variables of the system. As with the canonical ensemble, the thermodynamic quantities are not fixed, but have a statistical distribution about a mean or expected value.
Relation to potential VFor the case of a non-interacting gas, using the "Semiclassical Approach" we can write (approximately) the inverse of the potential in the form:
supposing that the Hamiltonian of every particle is H=T+V . DiscussionBefore specific results can be obtained from the grand canonical partition function, the energy levels of the system under consideration need to be specified. For example, the particle in a box model or particle in a harmonic oscillator well provide a particular set of energy levels and are a convenient way to discuss the properties of a quantum fluid. (See the gas in a box and gas in a harmonic trap articles for a description of quantum fluids.) These results may be used to construct the grand partition function to describe an ideal Bose gas or Fermi gas, and can be used as well to describe a classical ideal gas. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Partition_function_(statistical_mechanics)". A list of authors is available in Wikipedia. |





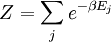
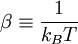
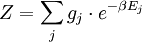 ,
,
![Z=\frac{1}{N!\,h^{3N}} \int \, \exp[-\beta H(p_1 \cdots p_N, x_1 \cdots x_N)] \; \mathrm{d}^3p_1 \cdots \mathrm{d}^3p_N \, \mathrm{d}^3x_1 \cdots \mathrm{d}^3x_N](images/math/a/5/2/a52e48ca64dafa4bc6e1509eb8fd0f6b.png)
 ,
instead of
,
instead of
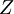 ,
which is used to denote a different quantity called
,
which is used to denote a different quantity called
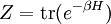
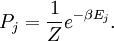
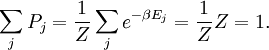
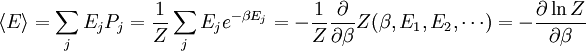
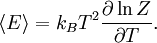
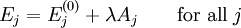
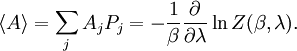
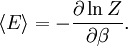
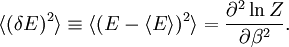
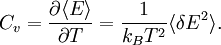
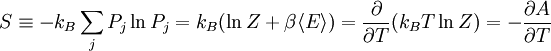
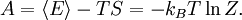
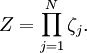
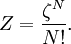
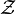 for an ideal quantum gas is written:
for an ideal quantum gas is written:
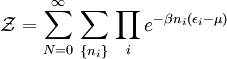
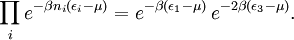
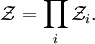
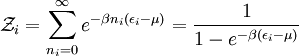
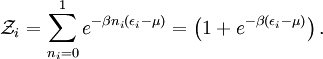
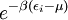 by ni!.
by ni!.
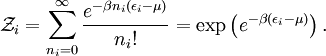
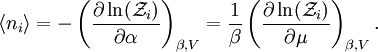
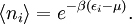
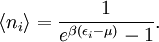
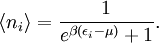
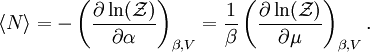
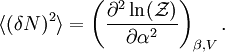
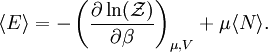
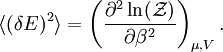
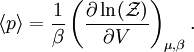
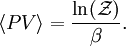
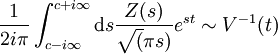
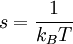 (valid for high T )
(valid for high T )


