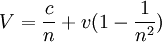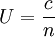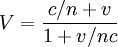To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Aether drag hypothesisThe aether drag hypothesis was an early attempt to explain the way experiments such as Arago's experiment showed that the speed of light is constant. The aether drag hypothesis is now considered to be incorrect by mainstream science. Product highlightAccording to the aether drag hypothesis light propagates in a special medium, the aether, that remains attached to things as they move. If this is the case then, no matter how fast the earth moves around the sun or rotates on its axis, light on the surface of the earth would travel at a constant velocity. The primary reason the aether drag hypothesis is considered invalid is because of the occurrence of stellar aberration. In stellar aberration the position of a star when viewed with a telescope swings each side of a central position by about 20.5 seconds of arc every six months. This amount of swing is the amount expected when considering the speed of earth's travel in its orbit. In 1871 Airy demonstrated that stellar aberration occurs even when a telesope is filled with water. It seems that if the aether drag hypothesis were true then stellar aberration would not occur because the light would be travelling in the aether which would be moving along with the telescope. If you visualize a bucket on a train about to enter a tunnel and a drop of water drips from the tunnel entrance into the bucket at the very center, the drop will not hit the center at the bottom of the bucket. The bucket is the tube of a telescope, the drop is a photon and the train is the earth. If aether is dragged then the droplet would be traveling with the train when it is dropped and would hit the center of bucket at the bottom. However, some modified versions of the hypothesis are still held by some dissidents that argue that aether drag may happen on a global (or larger) scale and the aberration is merely transferred into the entrained "bubble" around the earth which then faithfully carries the modified angle of incidence directly to the observer. This larger entrainment effect was believed by some scientists such as Dayton Miller who continued the search for aether many years after the widespread acceptance of relativity. The amount of stellar aberration, α, is given by: tan(α) = vδt / cδt So: tan(α) = v / c The speed at which the earth goes round the sun, v = 30 km/s, and the speed of light is c = 299,792,458 m/s which gives α = 20.5 seconds of arc every six months. This amount of aberration is observed and this contradicts the aether drag hypothesis. In 1818 Fresnel introduced a modification to the aether drag hypothesis that only applies to the interface between media. This was accepted during much of the nineteenth century but has now been replaced by special theory of relativity (see below). Historical importanceThe aether drag hypothesis is historically important because it was one of the reasons why Newton's corpuscular theory of light was replaced by the wave theory and it is used in early explanations of light propagation without relativity theory. It originated as a result of early attempts to measure the speed of light. In 1810 François Arago realised that variations in the refractive index of a substance predicted by the corpuscular theory would provide a useful method for measuring the velocity of light. These predictions arose because the refractive index of a substance such as glass depends on the ratio of the velocities of light in air and in the glass. Arago attempted to measure the extent to which corpuscles of light would be refracted by a glass prism at the front of a telescope. He expected that there would be a range of different angles of refraction due to the variety of different velocities of the stars and the motion of the earth at different times of the day and year. Contrary to this expectation he found that that there was no difference in refraction between stars, between times of day or between seasons. All Arago observed was ordinary stellar aberration. In 1818 Augustin Jean Fresnel examined Arago's results using a wave theory of light. He realised that even if light were transmitted as waves the refractive index of the glass-air interface should have varied as the glass moved through the aether to strike the incoming waves at different velocities when the earth rotated and the seasons changed. Fresnel proposed that the glass prism would carry some of the aether along with it so that "..the aether is in excess inside the prism". He realised that the velocity of propagation of waves depends on the density of the medium so proposed that the velocity of light in the prism would need to be adjusted by an amount of 'drag'. The velocity of light vn in the glass without any adjustment is given by: vn = c / n The drag adjustment vd is given by:
Where ρe is the aether density in the environment, ρg is the aether density in the glass and v is the velocity of the prism with respect to the aether. The factor The velocity of light in the glass is then given by:
This correction was successful in explaining the null result of Arago's experiment. It introduces the concept of a largely stationary aether that is dragged by substances such as glass but not by air. Its success favoured the wave theory of light over the previous corpuscular theory. The Fresnel drag coefficient was confirmed by an interferometer experiment performed by Fizeau. Water was passed at high speed along two glass tubes that formed the optical paths of the interferometer and it was found that the fringe shifts were as predicted by the drag coefficient. The special theory of relativity predicts the result of the Fizeau experiment from the velocity addition theorem without any need for an aether. If V is the velocity of light relative to the Fizeau apparatus and U is the velocity of light relative to the water and v is the velocity of the water:
which, if v/c is small can be expanded using the binomial expansion to become:
This is identical to Fresnel's equation. It may appear as if Fresnel's analysis can be substituted for the relativistic approach, however, more recent work has shown that Fresnel's assumptions should lead to different amount of aether drag for different frequencies of light and violate Snell's law (see Ferraro and Sforza (2005)). The aether drag hypothesis was one of the arguments used in an attempt to explain the Michelson-Morley experiment before the widespread acceptance of the special theory of relativity. Bibliography and References
See also
Categories: Aether theories | Obsolete scientific theories |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Aether_drag_hypothesis". A list of authors is available in Wikipedia. |




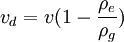
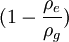 can be written as
can be written as 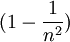 because the refractive index, n, would be dependent on the density of the aether. This is known as the Fresnel drag coefficient.
because the refractive index, n, would be dependent on the density of the aether. This is known as the Fresnel drag coefficient.