To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ensemble averageIn statistical mechanics, the ensemble average is defined as the mean of a quantity that is a function of the micro-state of a system (the ensemble of possible states), according to the distribution of the system on its micro-states in this ensemble. Since the Ensemble average is dependent of the ensemble chosen, its mathematical expression varies from ensemble to ensemble. However, the mean obtained for a given physical quantity doesn't depend on the ensemble chosen at the thermodynamic limit. Statistical ensemble (mathematical physics) Product highlight
Canonical ensemble averageclassical statistical mechanicsFor a classical system in thermal equilibrium with its environment, the ensemble average takes the form of an integral over the phase space of the system:
The denominator in this expression is known as the partition function, and is denoted by the letter Z. quantum statistical mechanicsFor a quantum system in thermal equilibrium with its environment, the weighted average takes the form of a sum over quantum energy states, rather than a continuous integral: characterization of the classical limitEnsemble average in other ensemblesMicrocanonical ensembleMacrocanonical ensemble |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ensemble_average". A list of authors is available in Wikipedia. |





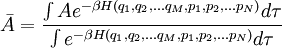
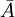 is the ensemble average of the system property A,
is the ensemble average of the system property A,
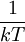 , known as
, known as 

