To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Virial expansionThe classical virial expansion expresses the pressure of a many-particle system in equilibrium as a power series in the density. The virial expansion was introduced in 1901 by Heike Kamerlingh Onnes as a generalization of the ideal gas law. He wrote for a gas containing N atoms or molecules, Product highlightwhere kB is the Boltzmann constant, T the absolute temperature, and
Writing β = (kBT) − 1, the virial expansion can be written in closed form as
The virial coefficients Bi(T) are characteristic of the interactions between the particles in the system and in general depend on the temperature T. See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Virial_expansion". A list of authors is available in Wikipedia. |


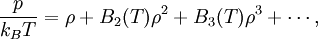



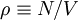 is the number density of the
gas.
Note that for a gas containing
is the number density of the
gas.
Note that for a gas containing 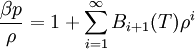 .
.


