To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Radial distribution functionIn computational mechanics and statistical mechanics, a radial distribution function (RDF), g(r), describes how the density of surrounding matter varies as a function of the distance from a distinguished point. Suppose, for example, that we choose a molecule at some point O in the volume. What is then the average density at some point P at a distance r away from O? If ρ = N / V is the average density, then the mean density at P given that there is a molecule at O would differ from ρ by some factor g(r). One could say that the radial distribution function takes into account the correlations in the distribution of molecules arising from the forces they exert on each other: (mean local density at distance r from O) = ρg(r) (1) As long as the gas is dilute the correlations in the positions of the molecules that g(r) takes into account are due to the potential φ(r) that a molecule at P feels owing to the presence of a molecule at O. Using the Boltzmann distribution law:
If φ(r) was zero for all r - i.e., if the molecules did not exert any influence on each other g(r) = 1 for all r. Then from (1) the mean local density would be equal to the mean density ρ: the presence of a molecule at O would not influence the presence or absence of any other molecule and the gas would be ideal. As long as there is a φ(r) the mean local density will always be different from the mean density ρ due to the interactions between molecules. When the density of the gas gets higher the so called low-density limit (2) is not applicable anymore because the molecules attracted to and repelled by the molecule at O also repel and attract each other. The correction terms needed to correctly describe g(r) resembles the virial equation, it is an expansion in the density:
in which additional functions Given a potential energy function, the radial distribution function can be found via computer simulation methods like the Monte Carlo method. It could also be calculated numerically using rigorous methods obtained from statistical mechanics like the Perckus-Yevick approximation. Product highlight
Importance of g(r)g(r) is of fundamental importance in thermodynamics for macroscopic thermodynamic quantities can be calculated using g(r). A few examples: The virial equation for the pressure:
The energy equation:
ExperimentalIt is possible to measure g(r) experimentaly with neutron scattering or x-ray scattering diffraction data. In such an experiment, a sample is bombarded with neutrons or x-ray which then diffract to all directions. The average molecular density at each distance can be extracted in according to Snells law: r=wavelength/sin(scattered angle), where r is the distance the neutron traveled during diffraction. Formal derivationConsider a system of N particles in a volume V and at a temperature T. The probability of finding molecule 1 in dr1, molecule 2 in dr2, etc., is given by
where ZN is the configurational integral. To obtain the probability of finding molecule 1 in dr1 and molecule n in drn, irrespective of the remaining N-n molecules, one has to integrate (7) over the coordinates of molecule n + 1 through N:
Now the probability that any molecule is in dr1 and any molecule in drn, irrespective of the rest of the molecules, is
For n = 1 the one particle distribution function is obtained which, for a crystal, is a periodic function with sharp maxima at the lattice sites. For a (homogeneous) liquid:
It is now time to introduce a correlation function g(n) by
g(n) is called a correlation function since if the molecules are independent from each other ρ(n) would simply equal ρn and therefore g(n) corrects for the correlation between molecules. From (9) it can be shown that
In the theory of liquids g(2)(r1,r2) is of special importance for it can be determined experimentally using X-ray diffraction. If the liquid contains spherically symmetric molecules g(2)(r1,r2) depends only on the relative distance between molecules, r12. People usually drop the subscripts: g(r) = g(2)(r12). Now ρg(r)dr is the probability of finding a molecule at r given that there is a molecule at the origin of r. Note that this probability is not normalized:
In fact, equation 13 gives us the number of molecules between r and r + d r about a central molecule. As of current, information on how to obtain the higher order distribution functions (g(3)(r1,r2,r3), etc.) is not known and scientists rely on approximations based upon statistical mechanics. References
Categories: Statistical mechanics | Physical chemistry |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Radial_distribution_function". A list of authors is available in Wikipedia. |


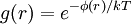 (2)
(2)
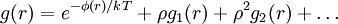 (3)
(3)
 appear which may depend on temperature
appear which may depend on temperature 


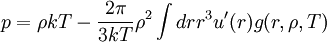 (4)
(4)
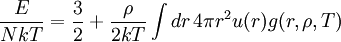 (5)
(5)
![kT\left(\frac{\partial \rho}{\partial p}\right)=1+\rho \int d r [g(r)-1]](images/math/7/3/9/7398478c87fd42d409c1fda60f0c2b07.png) (6)
(6)
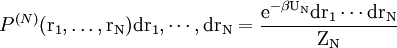 (7)
(7)
 (8)
(8)
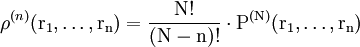 (9)
(9)
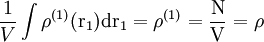 (10)
(10)
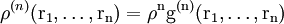 (11)
(11)
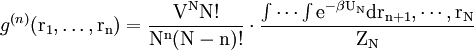 (12)
(12)
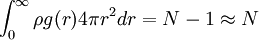 (13)
(13)


