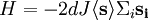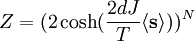To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Mean field theoryA many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases (Gaussian field theory, 1D Ising model.) The great difficulty (e.g. when computing the partition function of the system) is the treatment of combinatorics generated by the interaction terms in the Hamiltonian when summing over all states. The goal of mean field theory (MFT, also known as self-consistent field theory) is to resolve these combinatorial problems. Product highlightThe main idea of MFT is to replace all interactions to any one body with an average or effective interaction. This reduces any multi-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a relatively low cost. In field theory, the Hamiltonian may be expanded in terms of the magnitude of fluctuations around the mean of the field. In this context, MFT can be viewed as the "zeroth-order" expansion of the Hamiltonian in fluctuations. Physically, this means a MFT system has no fluctuations, but this coincides with the idea that one is replacing all interactions with a "mean field". Quite often, in the formalism of fluctuations, MFT provides a convenient launch-point to studying first or second order fluctuations. In general, dimensionality plays a strong role in determining whether a mean-field approach will work for any particular problem. In MFT, many interactions are replaced by one effective interaction. Then it naturally follows that if the field or particle exhibits many interactions in the original system, MFT will be more accurate for such a system. This is true in cases of high dimensionality, or when the Hamiltonian includes long-range forces. The Ginzburg criterion is the formal expression of how fluctuations render MFT a poor approximation, depending upon the number of spatial dimensions in the system of interest. While MFT arose primarily in the field of Statistical Mechanics, it has more recently been applied elsewhere, for example for doing Inference in Graphical Models theory in artificial intelligence. Formal approachThe formal basis for mean field theory is the Bogoliubov inequality. This inequality states that the free energy of a system with Hamiltonian has the following upper bound: where the average is taken over the equilibrium ensemble of the reference system with Hamiltonian
For the most common case that the target Hamiltonian contains only pairwise interactions, i.e., where where
Thus In order to minimize we take the derivative with respect to the single degree-of-freedom probabilities where the mean field is given by ExampleConsider the Ising model on an N-dimensional cubic lattice. The Hamiltonian is given by where the Σ' indicates summation over nearest neighbors, and Let's transform our spin variable by introducing the fluctuation from its mean value where we define If fluctuations are small, we may neglect this last term. As per the above arguments, when the fluctuations are small, then MFT should work 'better', from an intuitive stand-point. Again, the summand can be reexpanded to The only term that matters from the partition function's point of view is the first product. By symmetry arguments, the mean value of each spin is site-independent. We can replace We are still stuck with a double summation over neighboring spins, yet the summand involves only one site of each neighbor. Roughly speaking, we count 2d bonds (where d is the dimensionality of the cubic lattice) for each site. But since each bond participates in two spins, we would be overcounting by a factor of 2 if we gave each site a multiplicity of 2d. Therefore, the Hamiltonian becomes At this point, the Hamiltonian has been reduced to that of a single-body problem. The drawback is that now the effective coupling constant contains the mean value of the summand. Substituting this Hamiltonian into the partition function, and solving the effective 1D problem, we obtain where N is the number of lattice sites. This is a closed and exact expression for the partition function of the system. We may obtain the free energy of the system, and calculate critical exponents. MFT is known under a great many names and guises. Similar techniques include Bragg-Williams approximation, models on Bethe lattice, Landau theory, Flory-Huggins solution theory, and Scheutjens-Fleer theory. |
||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Mean_field_theory". A list of authors is available in Wikipedia. |





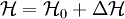
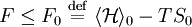
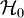 . In the special case that the reference Hamiltonian is that of a non-interacting system and can thus be written as
. In the special case that the reference Hamiltonian is that of a non-interacting system and can thus be written as
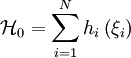
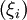 is shorthand for the degrees of freedom of the individual components of our statistical system (atoms, spins and so forth). One can consider sharpening the upper bound by minimising the right hand side of the inequality. The minimizing reference system is then the "best" approximation to the true system using non-correlated degrees of freedom, and is known as the mean field approximation.
is shorthand for the degrees of freedom of the individual components of our statistical system (atoms, spins and so forth). One can consider sharpening the upper bound by minimising the right hand side of the inequality. The minimizing reference system is then the "best" approximation to the true system using non-correlated degrees of freedom, and is known as the mean field approximation.
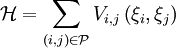
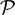 is the set of pairs that interact. The minimizing procedure can be carried out formally. Define
is the set of pairs that interact. The minimizing procedure can be carried out formally. Define 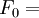
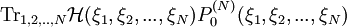
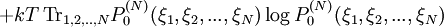
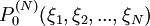 is the probability to find the reference system in the state specified by the variables
is the probability to find the reference system in the state specified by the variables 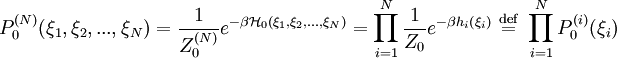 .
.
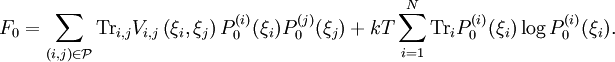
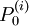 using a Lagrange multiplier to ensure proper normalisation. The end result is the set of self-consistency equations
using a Lagrange multiplier to ensure proper normalisation. The end result is the set of self-consistency equations
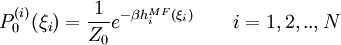
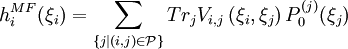
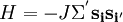
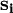 and
and 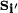 are neighboring Ising spins.
are neighboring Ising spins.
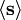 .
We may rewrite the Hamiltonian:
.
We may rewrite the Hamiltonian:
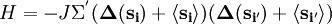
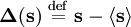 ; this is the fluctuation term of the spin.
If we multiply out the RHS, we obtain one term that's entirely dependent on the mean values of the spins, and independent of the spin configurations. This is the trivial term, which does not affect the
; this is the fluctuation term of the spin.
If we multiply out the RHS, we obtain one term that's entirely dependent on the mean values of the spins, and independent of the spin configurations. This is the trivial term, which does not affect the 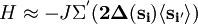
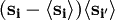
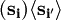
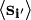 with
with