To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Landau theoryLandau theory in physics was introduced by Lev Davidovich Landau in an attempt to formulate a general theory of second-order phase transitions. He was motivated to suggest that the free energy of any system should obey two conditions: that the free energy is analytic, and that it obeys the symmetry of the Hamiltonian. Product highlightGiven these two conditions, one can write down a phenomenological expression for the free energy as a Taylor expansion in the order parameter. For example, the Ising model free energy may be written as the following: where the parameter for physical reasons. The variable Ψ is the coarse-grained field of spins, known as the order parameter or the total magnetization. This theory of Landau first raised the order parameter to prominence. Note that the Ising model exhibits the following discrete symmetry: If every spin in the model is flipped, such that Landau theory has been extraordinarily useful. While the exact values of the parameters r and s were unknown, critical exponents could still be calculated with ease, and only depend on the original assumptions of symmetry and analyticity. For the Ising model case, the equilibrium magnetization Ψ assumes the following value below the critical temperature Tc: At the time, it was known experimentally that the liquid-gas coexistence curve and the ferromagnet magnetization curve both exhibited a scaling relation of the form | T − Tc | β, where β was mysteriously the same for both systems. This is the phenomenon of universality. It was also known that simple liquid-gas models are exactly mappable to simple magnetic models, which implied that the two systems possess the same symmetries. It then followed from Landau theory why these two apparently disparate systems should have the same critical exponents, despite having different microscopic parameters. It is now known that the phenomenon of universality arises for other reasons. In fact, Landau theory predicts the incorrect critical exponents for the Ising and liquid-gas systems. The extension of Landau theory to include fluctuations in the order parameter shows why Landau theory is only valid near the critical points of systems with spatial dimensions of 4 or higher. This fact is connected to the idea that Landau theory is a mean field theory. Perhaps another great drawback of Landau theory is the requirement of analyticity for the free energy; this is directly at odds with the phenomenon of phase transitions, in which one frequently observes discontinuities or divergences in derivatives of the free energy. Landau's theory for phase transitions was to provide inspiration for another theory, the Ginzburg-Landau theory of superconductivity. Categories: Statistical mechanics | Condensed matter physics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Landau_theory". A list of authors is available in Wikipedia. |





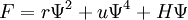
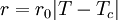
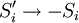 , where
, where