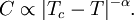To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Phase transitionIn thermodynamics, phase transition or phase change is the transformation of a thermodynamic system from one phase to another. The distinguishing characteristic of a phase transition is an abrupt change in one or more physical properties, in particular the heat capacity, with a small change in a thermodynamic variable such as the temperature. In the English vernacular, the term is most commonly used to describe transitions between solid, liquid and gaseous states of matter, in rare cases including plasma. Product highlight
Types of phase transition
Examples of phase transitions include:
Phase transitions happen when the free energy of a system is non-analytic for some choice of thermodynamic variables - see phases. This non-analyticity generally stems from the interactions of an extremely large number of particles in a system, and does not appear in systems that are too small. It is sometimes possible to change the state of a system non-adiabatically in such a way that it can be brought past a phase transition without undergoing a phase transition. The resulting state is metastable i.e. not theoretically stable, but quasistable. See superheating, supercooling and supersaturation. Classification of phase transitionsEhrenfest classificationThe first attempt at classifying phase transitions was the Ehrenfest classification scheme, which grouped phase transitions based on the degree of non-analyticity involved. Though useful, Ehrenfest's classification is flawed, as will be discussed in the next section. Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with a thermodynamic variable. The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density (which is the first derivative of the free energy with respect to chemical potential.) Second-order phase transitions have a discontinuity in a second derivative of the free energy. These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions. Modern classification of phase transitionsThe Ehrenfest scheme is an inaccurate method of classifying phase transitions, for it does not take into account the case where a derivative of free energy diverges (which is only possible in the thermodynamic limit). For instance, in the ferromagnetic transition, the heat capacity diverges to infinity. In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes: The first-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy. Because energy cannot be instantaneously transferred between the system and its environment, first-order transitions are associated with "mixed-phase regimes" in which some parts of the system have completed the transition and others have not. This phenomenon is familiar to anyone who has boiled a pot of water: the water does not instantly turn into gas, but forms a turbulent mixture of water and water vapor bubbles. Mixed-phase systems are difficult to study, because their dynamics are violent and hard to control. However, many important phase transitions fall in this category, including the solid/liquid/gas transitions and Bose-Einstein condensation. The second class of phase transitions are the continuous phase transitions, also called second-order phase transitions. These have no associated latent heat. Examples of second-order phase transitions are the ferromagnetic transition and the superfluid transition. Several transitions are known as the infinite-order phase transitions. They are continuous but break no symmetries. The most famous example is the Kosterlitz-Thouless transition in the two-dimensional XY model. Many quantum phase transitions in two-dimensional electron gases belong to this class. Properties of phase transitionsCritical pointsIn any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent. This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid, due to density fluctuations at all possible wavelengths (including those of visible light). During a phase change, the temperature of the sample does not change until the phase change is complete. SymmetryPhase transitions often (but not always) take place between phases with different symmetry. Consider, for example, the transition between a fluid (i.e. liquid or gas) and a crystalline solid. A fluid, which is composed of atoms arranged in a disordered but homogeneous manner, possesses continuous translational symmetry: each point inside the fluid has the same properties as any other point. A crystalline solid, on the other hand, is made up of atoms arranged in a regular lattice. Each point in the solid is not similar to other points, unless those points are displaced by an amount equal to some lattice spacing. Generally, we may speak of one phase in a phase transition as being more symmetrical than the other. The transition from the more symmetrical phase to the less symmetrical one is a symmetry-breaking process. In the fluid-solid transition, for example, we say that continuous translation symmetry is broken. The ferromagnetic transition is another example of a symmetry-breaking transition, in this case the symmetry under reversal of the direction of electric currents and magnetic field lines. This symmetry is referred to as "up-down symmetry" or "time-reversal symmetry". It is broken in the ferromagnetic phase due to the formation of magnetic domains containing aligned magnetic moments. Inside each domain, there is a magnetic field pointing in a fixed direction chosen spontaneously during the phase transition. The name "time-reversal symmetry" comes from the fact that electric currents reverse direction when the time coordinate is reversed. The presence of symmetry-breaking (or nonbreaking) is important to the behavior of phase transitions. It was pointed out by Landau that, given any state of a system, one may unequivocally say whether or not it possesses a given symmetry. Therefore, it cannot be possible to analytically deform a state in one phase into a phase possessing a different symmetry. This means, for example, that it is impossible for the solid-liquid phase boundary to end in a critical point like the liquid-gas boundary. However, symmetry-breaking transitions can still be either first- or second-order. Typically, the more symmetrical phase is on the high-temperature side of a phase transition, and the less symmetrical phase on the low-temperature side. This is certainly the case for the solid-fluid and ferromagnetic transitions. This happens because the Hamiltonian of a system usually exhibits all the possible symmetries of the system, whereas the low-energy states lack some of these symmetries (this phenomenon is known as spontaneous symmetry breaking). At low temperatures, the system tends to be confined to the low-energy states. At higher temperatures, thermal fluctuations allow the system to access states in a broader range of energy, and thus more of the symmetries of the Hamiltonian. Order parametersThe order parameter is the quantity which is indeterminate at the critical point (the point of the phase transition). For the ferromagnetic case, it is the magnetic susceptibility. For solid/liquid or liquid/gas transitions, it is the density. When symmetry is broken, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. Such variables are examples of order parameters. An order parameter is a measure of the degree of order in a system; the extreme values are 0 for total disorder and 1 for complete order.[1] For example, an order parameter can indicate the degree of order in a liquid crystal. However, note that order parameters can also be defined for non-symmetry-breaking transitions. There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect lines. Relevance for cosmologySymmetry-breaking phase transitions play an important role in cosmology. It has been speculated that, in the hot early universe, the vacuum (i.e. the various quantum fields that fill space) possessed a large number of symmetries. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to understanding the asymmetry between the amount of matter and antimatter in the present-day universe (see electroweak baryogenesis.) Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson[2] and David Layzer [3]. See also Relational order theories.
Critical exponents and universality classesContinuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points. It turns out that continuous phase transitions can be characterized by parameters known as critical exponents. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature T of the system while keeping all the other thermodynamic variables fixed, and find that the transition occurs at some critical temperature Tc. When T is near Tc, the heat capacity C typically has a power law behaviour: The constant α is the critical exponent associated with the heat capacity. It is not difficult to see that it must be less than 0 in order for the transition to have no latent heat. Its actual value depends on the type of phase transition we are considering. For -1 < α < 0, the heat capacity has a "kink" at the transition temperature. This is the behavior of liquid helium at the "lambda transition" from a normal state to the superfluid state, for which experiments have found α = -0.013±0.003. At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample (see here). This experimental value of α agrees with theoretical predictions based on variational perturbation theory (see here). For 0 < α < 1, the heat capacity diverges at the transition temperature (though, since α < 1, the divergence is not strong enough to produce a latent heat.) An example of such behavior is the 3-dimensional ferromagnetic phase transition. In the three-dimensional Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent α ∼ 0.110. Some model systems do not obey this power law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are an exception to the rule. Real phase transitions exhibit power law behavior. Several other critical exponents - β, γ, δ, ν, and η - are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations such as β = γ / (δ − 1), ν = γ / (2 − η). It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid-gas critical point have been found to be independent of the chemical composition of the fluid. More amazingly, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and is insensitive to the underlying microscopic properties of the system. Phase-change data storageSeveral data-storage technologies use chalcogenide glass, which can be "switched" between two states, crystalline or amorphous, with the application of heat. Phase change and optical disc technologyPhase change technology is also used to write to optical discs, such as CD-RW or DVD-RW discs. This is accomplished by including both a read laser and a more powerful write laser inside the drive. The discs contain a layer of a crystalline material that, when hit by a pulse of laser light from the write laser, changes to an amorphous state, thus changing its reflectivity. A different pulse level will reverse the changes, thus erasing the recorded information. The read laser is not powerful enough to induce a phase change, but can be used by the drive to tell whether a bit is "on" or "off" based on an area of the disc's reflectivity. History of phase change optical disc technology
Phase-change memoryPhase-change memory (PRAM) is a kind of non-volatile computer memory. Prototype PRAM devices have demonstrated higher density and faster write times than flash memory. PRAM uses chalcogenide glass, the same material utilized in re-writable optical media (such as CD-RW and DVD-RW). The amorphous, high resistance state is used to represent a binary 1, and the crystalline, low resistance state represents a 0. Samsung, Intel, and STMicroelectronics demonstrated prototype PRAM devices in 2006, and announced plans for commercial productions. See also
References
General references
|
|||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Phase_transition". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||